1量子ビット#

ここから先はさきほど学んだ量子を情報へつなげていきます．

1量子ビットの表記方法#

超伝導という方式の量子コンピュータでは電子がペアになった状態が回路上のある素子で，例えば電荷量子ビットという量子ビットでは左に偏っているか，右に偏っているかを\(0,1\)というラベルに対応させることが可能です．ブラケットの記法を使い，今回\(0,1\)に対応させる量子の状態を\(|0\rangle,|1\rangle\)と表記します．

古典的なコンピュータの情報の最小単位は\(0\)と\(1\)です．量子情報では上記の\(|0\rangle,|1\rangle\)をそのまま情報の最小単位として扱ってしまうのです．この先からは量子の状態である\(|0\rangle,|1\rangle\)をどのようにして扱うのか，量子の計算とは一体何なのか？に関して焦点を当てて説明をしていきます．

行列での表記方法#

(1)#\[\begin{align} |0\rangle & = \begin{bmatrix} 1 \\ 0 \end{bmatrix}\\ |1\rangle &= \begin{bmatrix} 0 \\ 1 \end{bmatrix} \end{align}\]

となります．また，\(|0\rangle,|1\rangle\)の係数である\(\alpha,\beta\)を用いると全体の波動関数は

(2)#\[\begin{align} |\psi\rangle = \alpha |0\rangle + \beta|1\rangle= \begin{bmatrix} \alpha\\ \beta \end{bmatrix}. \end{align}\]

と表され，規格化条件より

(3)#\[\begin{align} |\alpha|^2 + |\beta|^2 =1 \end{align}\]

となります．なお，\(\alpha,\beta\)のことを確率振幅と呼びます．
また，\(|0\rangle,|1\rangle\)は一次独立になっており，\(|0\rangle,|1\rangle\)の線形結合だけで空間全体を表現できるため，これらは基底であるともいえます．

測定#

量子力学では測定という動作によって量子の状態は収縮します．つまり，ある量子状態に対して\(1\)回だけ測定を行った時，\(1\)が得られるか\(0\)が得られるかどちらかの状況しか起こらなず波動関数は

(4)#\[\begin{align} |\psi\rangle\to \begin{cases} |0\rangle & 0観測した時\\ |1\rangle & 1を観測した時 \end{cases} \end{align}\]

と収縮します．前のセクションで説明したように

(5)#\[\begin{align} \alpha = \langle 0|\psi\rangle,\quad \beta = \langle 1|\psi\rangle \end{align}\]

とでき，それぞれ\(0,1\)を一回の測定で得られる確率(\(\text{Pr}(0),\text{Pr}(1)\))は複素振幅\(\alpha,\beta\)の絶対値の二乗になるため

(6)#\[\begin{align} \text{Pr}(0) &=\left|\alpha\right|^2=|\langle 0|\psi\rangle|^2 \\ \text{Pr}(1) &=\left|\beta\right|^2=|\langle 1|\psi\rangle|^2 \end{align}\]

{'1': 503, '0': 497}

以下は具体例です．

具体例

(7)#\[\begin{align} |\psi\rangle = \frac{1}{\sqrt{3}} |0\rangle +i \sqrt{\frac{2}{3}}|1\rangle \end{align}\]

の時それぞれ\(0,1\)を得る確率は

(8)#\[\begin{align} \text{Pr}(0) &= \left|\frac{1}{\sqrt{3}}\right|^2 = \frac{1}{3}\\ \text{Pr}(1) &= \left| i \sqrt{\frac{2}{3}}\right|^2 = \frac{2}{3} \end{align}\]

になります．

Bloch球(ブロッホ球)上での表現#

任意の量子状態は

(9)#\[\begin{align} \ket{\psi} = \alpha\ket{0} + \beta\ket{1} \quad (|\alpha|^2 + |\beta|^2 = 1) \end{align}\]

と表せるのでした． \(|\alpha|^2 + |\beta|^2 = 1\) の条件から実数のパラメータ \(\theta , \phi\) を用いて \( 0 \le \theta \le \pi, 0 \le \phi \le 2\pi \) の範囲のもとで

(10)#\[\begin{align} \ket{\psi} = \cos{\frac{\theta}{2}}\ket{0} + e^{i\phi}\sin{\frac{\theta}{2}}\ket{1} \end{align}\]

と量子状態を表すことができます．(簡単のためglobal phaseと呼ばれる位相は無視しています．) \(\phi\) はrelative phase(相対的位相)と呼ばれます．導入した \(\theta,\phi\) は以下の図のように3次元単位球の極座標表示におけるパラメータと同様の範囲を持つので，任意の量子状態を3次元の単位球面上の点 \((\sin{\theta}\cos{\phi}, \sin{\theta}\sin{\phi}, \cos{\theta})\) に対応付けられます．この単位球のことをBloch球と呼び，量子状態の幾何学的表現としてよく用います．

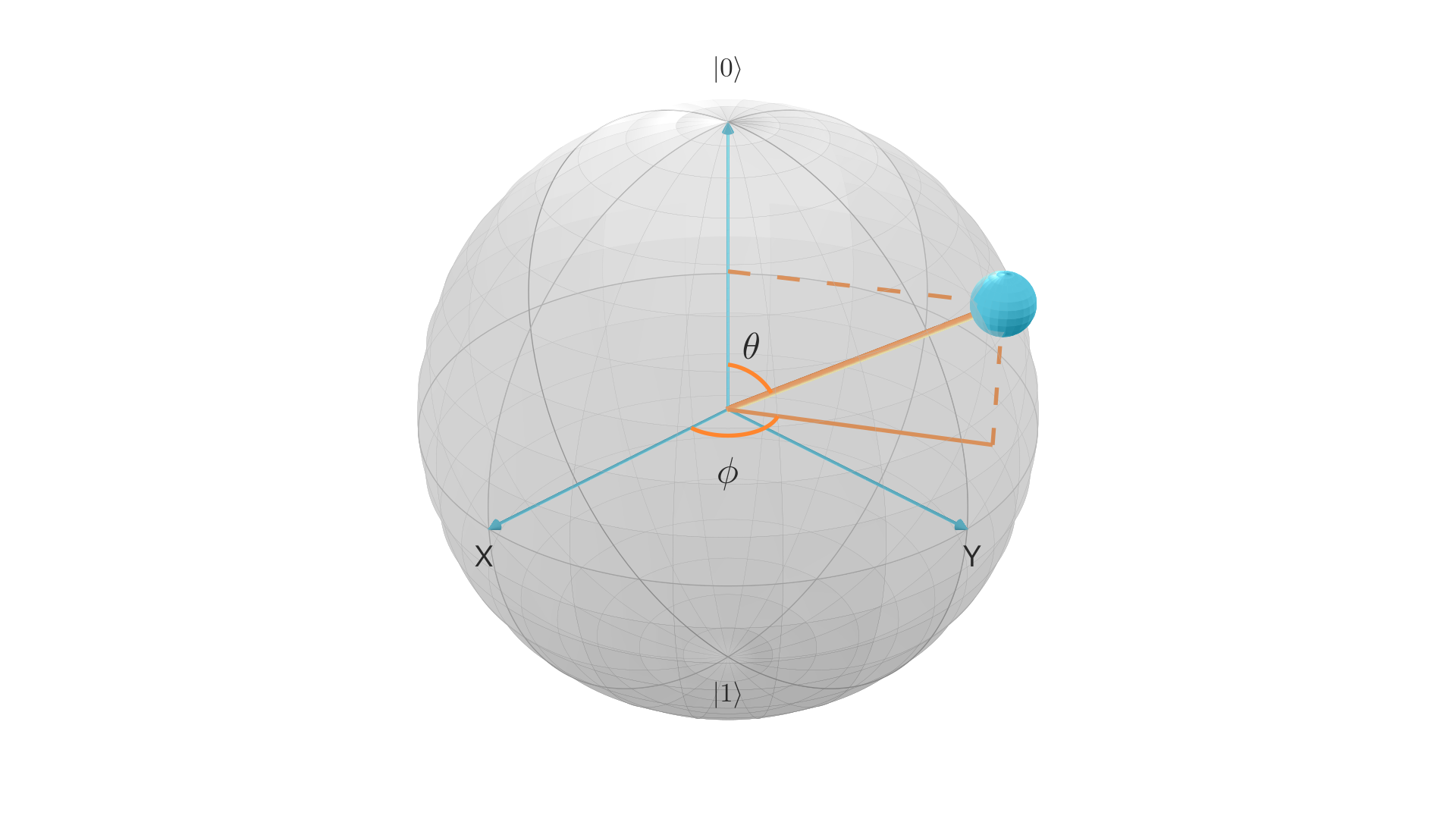
../../../_images/Bloch_expression.png — ブロッホ球#

Bloch球上での測定の可視化#

Bloch球上で表現された場合でも測定の原理は変わりません．繰り返し測定を行うと，それぞれ\(0,1\)の得られる確率分布を得ることができます．Bloch球上ではそれぞれ\(0,1\)が得られる確率はどのように表されるのでしょうか？

(11)#\[\begin{align} \ket{\psi} = \cos{\frac{\theta}{2}}\ket{0} + e^{i\phi}\sin{\frac{\theta}{2}}\ket{1} \end{align}\]

とした時，それぞれ\(0\)と\(1\)が得られる確率は以下の通りです：

(12)#\[\begin{align} \text{Pr}(0) &=\left| \langle 0|\psi\rangle \right|^2 = \left|\cos{\frac{\theta}{2}}\right|^2 = \cos^2{\frac{\theta}{2}} = \frac{1+\cos\theta}{2}\\ \text{Pr}(1) &=\left| \langle 1|\psi\rangle \right|^2 = \left|e^{i\phi}\sin{\frac{\theta}{2}} \right|^2 = \sin^2{\frac{\theta}{2}} = \frac{1-\cos\theta}{2} \end{align}\]

つまり，観測される確率は\(\phi\)の成分が消えることが分かります．
以下のアニメーションはある量子状態があった時，\(z\)軸に量子状態を射影した時のそれぞれの長さに比例していることが分かります．つまり，球体の頂点から量子状態の\(z\)成分までの長さは\(1\)を得る確率に比例し，逆の箇所は\(0\)を得る確率に比例しています．

単一量子ビットの計算#

ここから先は単一量子ビットを実際に変化させていきましょう！(古典では，足し算などの四則演算をNOTゲートなどの単純なゲートのみで表現することができました．量子ゲートは古典ゲートの量子版に当たるもので，目的の形に変化させること自体が実際の計算に当たります．)
すべての量子の操作は行列を作用させることで表現されます．例えば，量子ビット\(|0\rangle,|1\rangle\)を\(|1\rangle,|0\rangle\)にNOTゲートのように変化させる行列は

(13)#\[\begin{align} \begin{bmatrix} 0 & 1\\ 1 & 0 \end{bmatrix} \end{align}\]

で書かれてそれぞれ行列を作用させると以下のようになり，たしかにNOTゲートのように作用していることが分かります．

(14)#\[\begin{align} \underbrace{ \begin{bmatrix} 0 & 1\\ 1 & 0 \end{bmatrix} }_{NOTゲート} \underbrace{ \begin{bmatrix} 1\\ 0 \end{bmatrix} }_{|0\rangle} =\underbrace{ \begin{bmatrix} 0\\ 1 \end{bmatrix} }_{|1\rangle}, \quad \underbrace{ \begin{bmatrix} 0 & 1\\ 1 & 0 \end{bmatrix} }_{NOTゲート} \underbrace{ \begin{bmatrix} 0\\ 1 \end{bmatrix} }_{|1\rangle} = \underbrace{ \begin{bmatrix} 1\\ 0 \end{bmatrix} }_{|0\rangle} \end{align}\]

以上のように行列で量子状態を操作することができるのですが，操作後も量子の状態がBloch球上にいる必要があります．実際に作用させる行列はなんでも良いわけではなく，ユニタリ行列と呼ばれる行列を作用させる必要があります．このユニタリ行列を作用させた後でもBloch球上に量子状態がとどまります．

(もっと知りたい人のために) なぜユニタリ行列でないといけないか？の説明

操作をしてもBloch球上にとどまるようにしないといけないためには，ある行列\(U\)に対して\(|\psi' = U |\psi\rangle\)とすると，

(15)#\[\begin{align} \langle \psi'|\psi' \rangle = 1 \end{align}\]

と言う条件を満たす必要があります．書き換えると

(16)#\[\begin{align} \langle \psi |U^{\dagger} U |\psi\rangle = 1 \end{align}\]

であり，もとより，行列を作用させる前の量子の状態はBloch球上にいたため，

(17)#\[\begin{align} \langle \psi|\psi\rangle = 1 \end{align}\]

という条件は満たされていました．よって，行列の作用後にBloch球上にとどまるための条件は

(18)#\[\begin{align} U^{\dagger} U = I(単位行列) \end{align}\]

になります．これを満たすような行列のことをユニタリ行列と言い，ます．

量子ゲート#

特に量子ビットに作用する代表的なユニタリ行列のことを量子ゲートと呼びます．以下では代表的な量子ゲートをまとめています．

\(X\)ゲート#

\(X\)ゲートとは，先ほど説明したNOTゲートに対応しています．以下のアニメーションのように，ブロッホ球上で\(x\)軸を中心に\(\pi\)だけ回転させるゲートです．

\(Y\)ゲート#

\(Y\)ゲートとは，以下のアニメーションのように，ブロッホ球上で\(y\)軸を中心に\(\pi\)だけ回転させるゲートです．

\(Z\)ゲート#

\(Z\)ゲートとは，ブロッホ球上で\(z\)軸を中心に\(\pi\)だけ回転させるゲートです．行列の表記は

(19)#\[\begin{align} Z &= \begin{bmatrix} 1 & 0 \\ 0 & -1 \end{bmatrix}\\ Z |0\rangle &= |0\rangle, \quad Z |1\rangle =-|1\rangle \end{align}\]

\(H\)ゲート#

\(H\)ゲートは上記とは少し異なっています．\(H\)ゲートとは，ブロッホ球上で，\(x\)軸と\(z\)軸の中間となる軸を中心に\(\pi\)だけ回転させます．つまり．以下のアニメーションの軸を中心に状態を\(\pi\)だけ回転させるのです．

回転ゲート#

その他に代表的なゲートとして回転ゲートと呼ばれるゲートがあります．ブロッホ球上で\(x,y,z\)方向にそれぞれ\(\theta_x,\theta_y,\theta_z\)だけ回転するゲートは以下の通りです．

(20)#\[\begin{align} X_{\theta_x} &:= \exp\left( -\frac{i}{2} \theta_x X\right)= \begin{bmatrix} \cos\theta_x/2 & -i \sin\theta_x/2\\ -i \sin\theta_x/2 & \cos\theta_x/2 \end{bmatrix}\\ Y_{\theta_y} &:= \exp\left( -\frac{i}{2} \theta_y Y \right)= \begin{bmatrix} \cos\theta_y/2 & -\sin\theta_y/2\\ \sin\theta_y/2 & \cos\theta_y/2 \end{bmatrix}\\ Z_{\theta_z} &:= \exp\left( -\frac{i}{2} \theta_z Z\right) = \begin{bmatrix} e^{-i\theta_z/2} & 0\\ 0 & e^{i\theta_z/2} \end{bmatrix} \end{align}\]

なお，以上の\(\exp\)の部分から具体的な行列の形への変換の導出は以下の行列指数関数の性質1を利用して行っています．また，量子ゲートである\(X,Y,Z\)を恒等行列である

(21)#\[\begin{align} I = \begin{bmatrix} 1 & 0 \\ 0 & 1 \\ \end{bmatrix} \end{align}\]

の行列は以下のパウリ行列と呼ばれておりこれからの表記方法を以下にまとめています．

パウリ行列

パウリ行列とは以上で見てきた基本的な量子ゲートである\(X,Y,Z\)とのことを表し，まとめて\(\sigma_i, (i = \{ X,Y,Z,I \})\)などと表現します．

行列指数関数の性質1

パウリ行列\(\sigma_i\)に対して

(22)#\[\begin{align} \exp\left( -\frac{i}{2}\theta \sigma_i \right) = \cos( \theta/2 )\sigma_I - i \sin(\theta/2) \sigma_i \end{align}\]

となります．なお，\(\sigma_I\)は恒等行列\(I\)を表します．証明は以下の通りです：
指数関数を展開すると

(23)#\[\begin{align} &\exp\left( -\frac{i}{2}\theta \sigma_i \right)\\ \quad& = \sigma_I -\frac{i}{2}\theta \sigma_i + \frac{1}{2}\left( -\frac{i}{2}\theta \sigma_i \right)^2 +\frac{1}{6}\left( -\frac{i}{2}\theta \sigma_i\right)^3+ \cdots\\ \quad& = \sigma_I -\frac{i}{2}\theta \sigma_i - \frac{1}{2}\left( \frac{\theta}{2} \right)^2 \sigma_I +i\frac{1}{6}\left( \frac{\theta}{2} \right)^3\sigma_i+ \cdots\\ \quad& = \left\{ 1 - \frac{1}{2}\left( \frac{\theta}{2} \right)^2 + \cdots \right\}\sigma_I -i \left\{ \frac{\theta}{2}- \frac{1}{6}\left( \frac{\theta}{2} \right)^3+ \cdots \right\}\sigma_i\\ \quad &= \cos( \theta/2 )\sigma_I - i \sin(\theta/2) \sigma_i \end{align}\]

となります．ただし，パウリ行列の二乗は単位行列\(\sigma_I\)であるという性質を利用しています：

(24)#\[\begin{align} \left( \sigma_i\right)^2 &=\sigma_I \end{align}\]

その他のゲート#

その他に重要なゲートは\(S_X\)ゲートです．\(S_X\)ゲートは第二章で説明するトランズモン量子ビットで肝心であり，以下の行列で与えれます．

(25)#\[\begin{align} S_X = \frac{1}{2} \begin{bmatrix} 1+i & 1-i\\ 1-i & 1+i \end{bmatrix} = e^{i\pi/4}X_{\pi/2} \end{align}\]

ここで，\(S_X = e^{i\pi/4}X_{\pi/2}\)となりましたが，\(e^{i\pi/4}\)の部分はglobal位相に当たる部分であるため測定結果に影響を与えません．

超伝導方式の量子ゲートはシュレディンガー方程式の時間発展

始めてこの量子ゲートを学んだ時，理論的にはただの行列操作を行っているだけでこのようなゲート操作は本当に実装されているのか？もしできているとしたらどのように？とずっと疑問に思っていました．
しかし，次のように考えると超伝導方式の場合の量子ゲートの実装の概略が見えてきます．量子ビットと，量子ビットを操作する素子が何か実装できているとします，この時，量子ビットと操作する素子を含めたハミルトニアンを定義することができ，このハミルトニアンを時間積分して得られる時間発展演算子がそれぞれ\(X,Y,Z,H\)ゲートなどに当たるのです．(もちろんそれぞれのゲートでは，量子ビットを操作する素子にて，パルスの形，外部磁場などの操作できるものを設定しています．)
第二章ではこの話をより詳しく記載しています．

量子ゲートを複数回作用させてみる#

これまではそれぞれの量子ゲートに関して述べましたが，実際の量子コンピュータではこれらの量子ゲートを組み合わせることで量子の計算を行っています．
多えば\(|0\rangle\)の状態に量子ゲートを\(X\to Y\)の順番で複数回作用させ様子を模式化すると以下の通りになります．

(26)#\[\begin{align} \underbrace{X}_{2つ目の量子ゲート}\quad \underbrace{Y}_{1つ目の量子ゲート} |0\rangle &= \begin{bmatrix} 0 & 1 \\ 1 & 0 \end{bmatrix} \begin{bmatrix} 0 & -i\\ i & 0 \end{bmatrix} \begin{bmatrix} 1 \\ 0 \end{bmatrix}\\ &= \begin{bmatrix} i & 0\\ 0 & -i \end{bmatrix} \begin{bmatrix} 1 \\ 0 \end{bmatrix} = i \begin{bmatrix} 1 \\ 0 \end{bmatrix} = i|0\rangle \end{align}\]

となります．このようにして，複数の量子ゲートを作用させることが可能です．複数量子ゲートの様子を以下のアニメーションにしました．それぞれのゲートを作用させた後の状態を考えながらアニメーションを動かしてみてください．

状態を取り出す#

さきほど説明した測定では，Bloch球の\(z\)軸の成分である，\(\cos\theta\)の値を得ることができました．すると，「測定を通じて量子の状態がBloch球のどこにいるのかを推測ことは不可能なのでは？」と思うでしょう．(つまり，「測定」を行うと\(\theta\)は得られるが，\(\phi\)は得られてないため「測定」という過程ではBloch球で量子状態がどこにいるかを掌握することは不可能ではないか？ということです．)
しかし，量子状態がBloch球上でどの位置にいるのかは，正確な計算が行えているかどうかの判定や，実際の計算結果を取り出すために非常に重要な事柄です．実はさきほど説明した各量子ゲートを使うことによって量子状態がBloch球上のどこにいるのかを推定することが可能になるのです．

X 測定#

これまで\(z\)軸の成分を確率で取り出すことは可能であったためまずは\(x\)軸の成分を取り出すことを考えてみましょう．唐突ですが，ある量子状態：

(27)#\[\begin{align} |\psi\rangle = \cos\frac{\theta}{2}|0\rangle + e^{i\phi}\sin\frac{\theta}{2}|1\rangle \end{align}\]

に対して\(H\)ゲートを作用させて，それぞれ\(|0\rangle,|1\rangle\)の確率を取り出してみます:

(28)#\[\begin{align} H|\psi\rangle &= \frac{1}{\sqrt{2}}\cos\frac{\theta}{2}\left( |0\rangle + |1\rangle \right) +\frac{1}{\sqrt{2}}e^{i\phi} \sin\frac{\theta}{2}\left( |0\rangle - |1\rangle \right)\\ &= \frac{1}{\sqrt{2}}\left( \cos\frac{\theta}{2} + e^{i\phi}\sin\frac{\theta}{2} \right) |0\rangle + \frac{1}{\sqrt{2}} \left( \cos\frac{\theta}{2} - e^{i\phi} \sin\frac{\theta}{2} \right)|1\rangle \end{align}\]

となるので，それぞれの確率は

(29)#\[\begin{align} \text{Pr}(0) &= \left| \frac{1}{\sqrt{2}}\left( \cos\frac{\theta}{2} + e^{i\phi}\sin\frac{\theta}{2} \right) \right|^2 = \frac{ 1+ \sin\theta\cos\phi }{2}\\ \text{Pr}(1) &= \left| \frac{1}{\sqrt{2}} \left( \cos\frac{\theta}{2} - e^{i\phi} \sin\frac{\theta}{2} \right) \right|^2 = \frac{ 1- \sin\theta\cos\phi }{2} \end{align}\]

になります．極座標での\(x\)の値は\( \sin\theta\cos\phi \)となるので，\(H\)ゲートを通して測定を繰り返し，得られた統計データである\(\text{Pr}(0),\text{Pr}(1)\)から\(\text{Pr}(0)-\text{Pr}(1)\)を計算すると，量子状態のブロッホ球での\(x\)軸の成分を取り出せていることが分かります．

\(H\)ゲートというユニタリ行列は\(x,z\)軸を中心に量子状態を\(\pi\)だけ回転させる行列でした．ここでは，量子状態だけではなく，もともとあった座標も見かけ上回転させるとして\(H\)ゲートを作用させます．(実際には座標は回転しないためここでいう\(H\)ゲートが座標を回転させるような性質を持っているわけではないです．あくまで見かけ上です．)ここで，量子状態と，\(x\)軸のなす角を\(\theta_x\)とすると，内積より，

(30)#\[\begin{align} \cos\theta_x = \boldsymbol{e}_x \cdot \left( \sin\theta\cos\phi\boldsymbol{e}_x + \sin\theta\sin\phi\boldsymbol{e}_y+ \cos\theta\boldsymbol{e}_z \right) = \sin\theta\cos\phi \end{align}\]

であることを利用してアニメーションで表すと次のようになります．

Y測定#

\(Y\)測定は，先ほど説明した\(S_X\)ゲートというゲートを作用させることで実現できます．ある量子状態：

(31)#\[\begin{align} |\psi\rangle = \cos\frac{\theta}{2}|0\rangle + e^{i\phi}\sin\frac{\theta}{2}|1\rangle \end{align}\]

に対して作用させて計算をすると以下の通りになります．

(32)#\[\begin{align} S_X |\psi\rangle &= \frac{1}{2}\cos\frac{\theta}{2}\left\{ (1+i) |0\rangle + (1-i)|1\rangle \right\} +\frac{1}{2}e^{i\phi} \sin\frac{\theta}{2}\left\{ (1-i)|0\rangle + (1+i)|1\rangle \right\}\\ &= \frac{1}{2} \left\{ \cos\frac{\theta}{2}(1+i) + e^{i\phi} \sin\frac{\theta}{2}(1-i) \right\}|0\rangle + \frac{1}{2} \left\{ \cos\frac{\theta}{2}(1-i) + e^{i\phi} \sin\frac{\theta}{2}(1+i) \right\}|1\rangle \end{align}\]

となるためそれぞれ\(|0\rangle,|1\rangle\)を観測する確率は

(33)#\[\begin{align} \text{Pr}(0) &= \left| \frac{1}{2} \left\{ \cos\frac{\theta}{2}(1+i) + e^{i\phi} \sin\frac{\theta}{2}(1-i) \right\} \right|^2 = \frac{ 1+ \sin\theta\sin\phi }{2}\\ \text{Pr}(1) &= \left| \frac{1}{2} \left\{ \cos\frac{\theta}{2}(1-i) + e^{i\phi} \sin\frac{\theta}{2}(1+i) \right\} \right|^2 = \frac{ 1- \sin\theta\sin\phi }{2} \end{align}\]

になります．極座標での\(y\)の値は\( \sin\theta\sin\phi \)となるので，\(S_X\)ゲートを通して測定を繰り返し，得られた統計データである\(\text{Pr}(1),\text{Pr}(0)\)の\(\text{Pr}(0)-\text{Pr}(1)\)を計算すると，量子状態のブロッホ球での\(y\)軸の成分を取り出せていることが分かります．
イメージとしては以下のアニメーションになります：

以上より，測定から得られる統計データを下に量子状態を求められることが分かりました．

重要

仮に繰り返し同じ量子状態を生成して測定ができる場合，relative phase(相対的位相)を含めた量子状態を得ることができます：

(34)#\[\begin{align} \ket{\psi} = \cos{\frac{\theta}{2}}\ket{0} + e^{i\phi}\sin{\frac{\theta}{2}}\ket{1} \end{align}\]

また，このように一般的に量子の状態を測定を通じて再構築することを量子統計推定または量子状態トモグラフィーと言います．(ここで再構築と言っているのは人間が行う「測定」という行為によって量子状態が壊れてしまい，壊れてしまった量子状態を「測定」によって推定するという行為はまさしく再構築に値することだからです．)

1量子ビット

目次

1量子ビット#