超伝導量子回路の基礎

超電導量子ビットをよりよく理解するためには超電導量・LC共振器・ジョセフソン接合などの重要事項を説明する必要があります．そこで，本教材ではいきなり超電導量子ビットを出すことはせずまずはこれらの概念を説明し，次のセクションで超電導量子ビットに関して説明をしていきます：

超伝導

ある特定の物質を0Kに近い極低温に冷やすと超伝導という現象が起きます．そして，超伝導が起きる温度を臨界温度と言います．超伝導状態にある物質では様々な効果が現れるのですがここでは深い話は述べず，超伝導量子ビットにて説明をする際に必要となる現象のみをここでは述べます．詳しくは参考文献を参照してください．超伝導で重要となる性質は次の3つです．

• 抵抗値が\(0\Omega\)になる．

• 電子が二つペアなってクーパー対となる．

• 超伝導状態にあるリングの中を通る磁束の数が量子化される．

「抵抗値が\(0\Omega\)になる．」に関しては回路にて永久的に電流が流れることを意味します．また，「電子が二つペアなってクーパー対となる」に関しては以下のアニメーションのように超伝導状態にある物質では電子が二つ結合してクーパー対と呼ばれるペアを形成します．

注意

もちろん，実際の物理描像はこのようにはなっておらずあくまで分かりやすく説明するためのイメージです．

クーパー対によって電子が二つで一つとなるため，回路内の一つの粒子の電荷は\(-e\)から\(-2e\)になるため，この後説明するLC共振器も電子に注目したハミルトニアンではなく，クーパー対に対応するハミルトニアンに書き直す必要があります．

次に磁束の量子化に関して説明をしていきます．以下のようなリングを考えます．臨界温度(\(T_0\))と呼ばれる温度以上(\(T>T_0\))で外部磁場を印可させて，臨界温度以下(\(T<T_0\))にした状態で磁場を取り去らいます．この時，リングの内部には磁束が残ります．

何かしらの事情で磁束が残るという仮定をすると，通常であれば残る磁束は，外部磁束に対して連続に変化するはずです．しかし，リングが臨界温度以下で超伝導体であれば，実は，残る磁束は外部磁束に対して離散的になってしまうのです．この残る磁束は，

(1)\[\begin{align} \Phi = \Phi_0\cdot (整数) \end{align}\]

になり，離散的な値を取っていることが実験的にも理論的にも分かっています．(\(\Phi_0\)のことを磁束量子と言います．)
ミクロな世界で物理的な量が離散値となることを量子化と言い，この実験から超伝導体では磁束が量子化されていることが分かります．

LC共振器

以下の回路はLC共振器と呼ばれております．

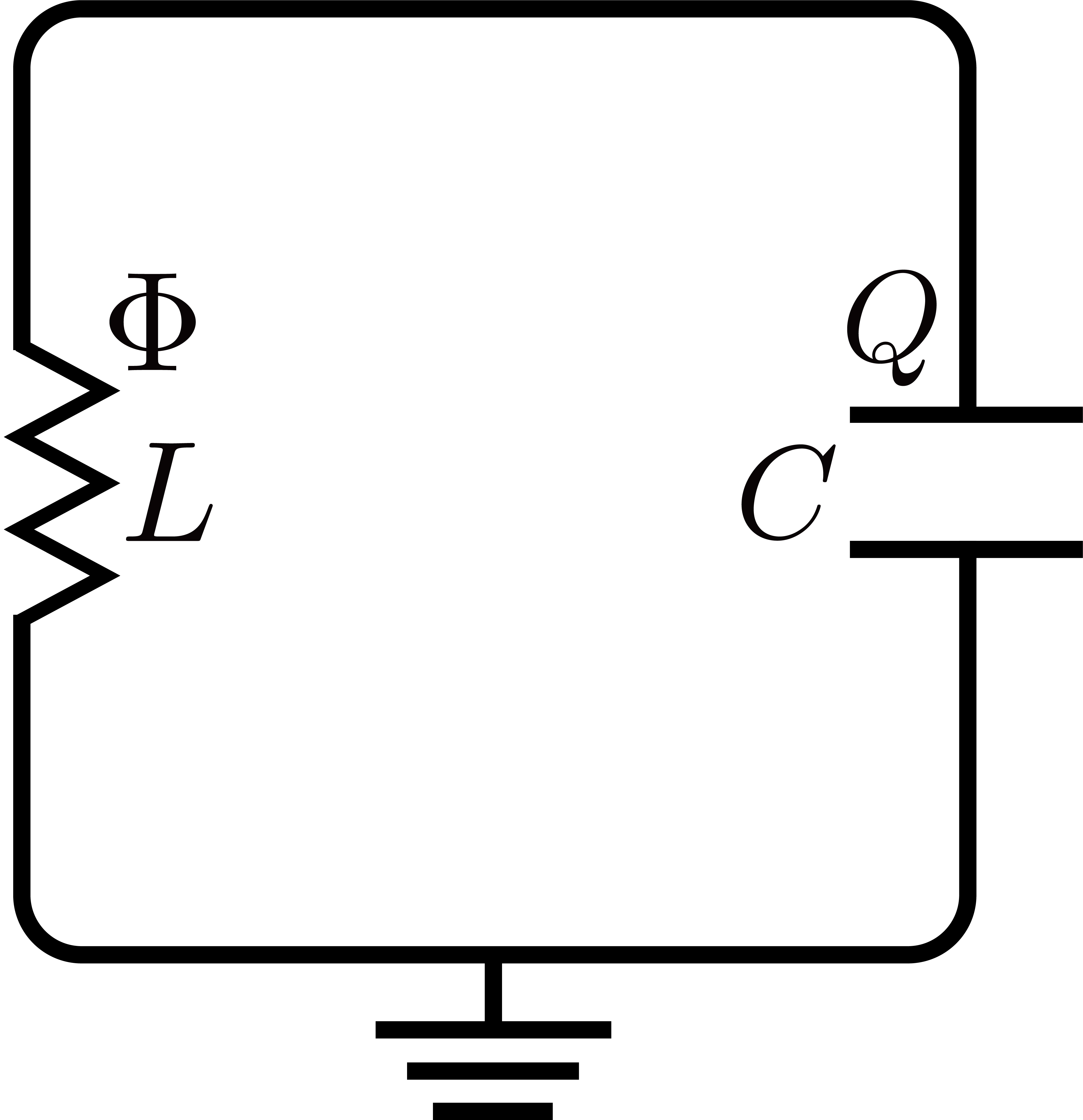
LC共振器の回路図

LC共振器は古典の場合だと，全体のエネルギーは

(2)\[\begin{align} E = \frac{1}{2L}\Phi^2 + \frac{Q^2}{2C} \end{align}\]

になります．しかし，先ほど説明したように，LC共振器が超伝導体になると，磁束はある特定の値しか持つことが許されません．つまり磁束が量子化され，磁束に対になっている量である電荷も量子化され，最終的にLC共振器全体のハミルトニアンは以下のようになります：

(3)\[\begin{align} H = \frac{1}{2L}\hat{\Phi}^2 + \frac{\hat{Q}^2}{2C} \end{align}\]

以下では古典のLC共振器の解析から量子LC共振器のエネルギーの導出を行っていますが本教材の想定レベルを超えるため飛ばしても構いません．

(もっと知りたい人のために)LC共振器の解析

古典の場合
まずは量子化をしていない場合を考えます．キャパシタ(コンデンサ)と，インダクタ(コイル)の電圧降下とキルヒホッフの法則より，

(4)\[\begin{align} L\frac{dI}{dt} + \frac{Q}{C} =0 \end{align}\]

となります．ここで両辺に\(I=\dot{Q}\)をかけると，

(5)\[\begin{align} \frac{d}{dt}\left( \frac{L}{2} I^2 + \frac{Q^2}{2C} \right) =0 \end{align}\]

になり，それぞれ，キャパシタのエネルギーと，インダクタのエネルギーは

(6)\[\begin{align} (キャパシタのエネルギー) &= \frac{Q^2}{2C}\\ (インダクタのエネルギー) &= \frac{L}{2} I^2 \end{align}\]

となります．また，コイルを貫く磁束\(\Phi\)は

(7)\[\begin{align} \Phi = LI \end{align}\]

です． よって，キャパシタのエネルギーを運動エネルギー，インダクタのエネルギーをポテンシャルとみることによって，ラグラジアンは

(8)\[\begin{align} L = \frac{1}{2}L\dot{Q}^2 - \frac{Q^2}{2C} \quad\because \dot{Q}=I \end{align}\]

になります．\(Q\)を粒子で言う位置の変数であるとすると，このラグラジアンの運動量に当たる成分は

(9)\[\begin{align} \frac{\partial L}{\partial \dot{Q}} = L\dot{Q} = LI = \Phi \end{align}\]

になります．よって，粒子で言う，\(x,p\)は回路で言うところの\(Q,\Phi\)に置き換えることができました．この事実を使ってラグラジアンをハミルトニアンに変形します：

(10)\[\begin{align} H(Q,\Phi) = \Phi\dot{Q} - L = \frac{1}{2L}\Phi^2 + \frac{Q^2}{2C} \end{align}\]

量子化をする
超伝導体になると，磁束\(\Phi\)が量子化すると話しました．(すなわち，磁束が許される値が連続値ではなくて，離散的な値になるということです．)もとより，\(\Phi = L\dot{Q}\)の関係式があったため，磁束が量子化されればそれに伴って\(Q\)も量子化されます．量子化をすると，変数は演算子に置き換わるため，

(11)\[\begin{align} Q \to \hat{Q}, \quad \Phi \to \hat{\Phi} \end{align}\]

になります．また，\(x,p\)は量子化をすると次の関係がありました：

(12)\[\begin{align} [ \hat{x},\hat{p} ] =\hat{x}\hat{p}-\hat{p}\hat{x} = i\hbar \end{align}\]

ここでは，\(x,p\)を\(Q,\Phi\)に対応づけることができたため，量子化すると，

(13)\[\begin{align} [ \hat{Q},\hat{\Phi} ] =\hat{Q}\hat{\Phi}-\hat{\Phi}\hat{Q} = i\hbar \end{align}\]

という条件が必要になります．よって，量子化された場合の回路のハミルトニアンは

(14)\[\begin{align} H = \frac{1}{2L}\hat{\Phi}^2 + \frac{\hat{Q}^2}{2C} \end{align}\]

になります．ここで，第三の条件の電子が二つペアになる条件を付けます．本来電荷\(Q\)は電子1個が持つ電荷\(-e\)に比例する項でしたが，今回はクーパー対によって電子が2個あるため，電荷は\(-2e\)に比例するため，\(\hat{\phi} = 2\pi\hat{\Phi}/\Phi_0,\quad \Phi_0 ＝ h/2e \), \(\hat{n}=\hat{Q}/2e\)と置き換えます．(\(\Phi_0\)は磁束量子と呼ばれています．詳しい話は参考文献を参考にしてください)すると，交換関係は

(15)\[\begin{align} [ \hat{\phi},\hat{n} ] = 2\pi/(\Phi_0 2e)\left[\hat{\Phi}\hat{Q}-\hat{\Phi}\hat{Q}\right] = 2\pi/(\Phi_0 2e)i\hbar = i \end{align}\]

となります．またハミルトニアンは

(16)\[\begin{align} H = 4E_c \hat{n}^2 + \frac{1}{2}E_L\hat{\phi}^2, \quad E_C = \frac{e^2}{2C} , E_L =\frac{(\Phi_0/2\pi)^2}{L} \end{align}\]

となります．ここで，調和振動子と同様にして，

(17)\[\begin{align} \hat{n} &= \left[ \frac{E_L}{32E_C} \right]^{1/4}\times i(\hat{a}-\hat{a}^{\dagger})\\ \hat{\phi} &= \left[ \frac{2E_C}{E_L} \right]^{1/4}\times (\hat{a}+\hat{a}^{\dagger}) \end{align}\]

とすると，

(18)\[\begin{align} H = \hbar\omega\left(\hat{a}^{\dagger}\hat{a}+\frac{1}{2}\right),\quad \omega = \frac{1}{\sqrt{LC}} \end{align}\]

となり，調和振動子と同様にして，エネルギーは

(19)\[\begin{align} E_n = \hbar\omega\left(n+\frac{1}{2}\right), \quad n = 0,1,2,\cdots \end{align}\]

となります．

そして，超伝導体である場合，先ほど説明したように電子はクーパー対を形成するため，ハミルトニアンをクーパー対に対応させ整理すると以下の通りになります：

(20)\[\begin{align} H = 4E_C \hat{n}^2 - \frac{1}{2}E_L \hat{\phi}^2 \end{align}\]

なお，

(21)\[\begin{align} E_C = \frac{e^2}{2C}, \quad E_L = \left( \frac{\Phi_0}{2\pi} \right)^2 \frac{1}{L},\quad, \hat{n} = \frac{\hat{Q}}{2e} , \quad \hat{\phi} = \frac{\Phi}{\Phi_0} \end{align}\]

としています．また，

(22)\[\begin{align} \Phi_0 = \frac{h}{2e} \end{align}\]

を磁束量子と言います．また，多少アドバンストな話をすると，

(23)\[\begin{align} \hat{n} &= \left[ \frac{E_L}{32E_C} \right]^{1/4}\cdot i (\hat{a}-\hat{a}^{\dagger}),\\ \hat{\phi} &= \left[ \frac{2E_C}{E_L} \right]^{1/4}\cdot (\hat{a}+\hat{a}^{\dagger}) \end{align}\]

とすると，

(24)\[\begin{align} H = \hbar\omega_r \left( \hat{a}^{\dagger} \hat{a} + \frac{1}{2} \right), \quad \omega_r = \frac{1}{\sqrt{LC}} \end{align}\]

となり，\(\hat{a}^{\dagger} \hat{a}\)は固有値が\(n = 0,1,2,\cdots\)であるため以下のように超伝導体のLC共振器のエネルギーは以下の通りになります．

量子LC共振器のエネルギー

(25)\[\begin{align} E = \hbar\omega_r\left(n+\frac{1}{2}\right), \quad n = 0,1,2,\cdots \end{align}\]

ジョセフソン接合

LC共振器が超伝導量体になるとエネルギーは離散的な値を取ることが分かりました．つまり，何かしらの方法でLC共振器のエネルギーを読み取ることができれば，量子ビットとして働くことができます．しかし一つだけ問題があります．それは，すべてのエネルギーの間隔が均一であるということです．量子ゲートのセクションで詳しく説明しますが，量子ビットの状態を遷移させる際にはそれぞれのエネルギー間隔に対応する周波数を持つパルスを当てる必要があり，すべてのエネルギー間隔が等しいと，\(E_0,E_1\)間の遷移であるはずなのに，\(E_1,E_2\)間の遷移も同時に起きてしまい，選択的に\(E_0\)と\(E_1\)の間だけを取り出すことが難しくなってしまうからです．そこで，この問題を解決するために登場するのがジョセフソン接合です．ジョセフソン接合が量子ビットにどう作用するかの詳細な説明は次のセクションに任せてここではジョセフソン接合の基本的な性質に関してみていきます．

以下の図のように，超伝導体の間に酸化被膜などの通常の電気を通さない「絶縁体」と呼ばれるを挟んだ構造をジョセフソン接合と言います．

ジョセフソン接合の模式図

先ほど説明したように，超伝導体になると，二つの電子がペアになるクーパー対を形成して，クーパー対が量子的な振る舞いをします．電子などの粒子はトンネル効果という現象によって絶縁体でも通り抜けることができるため，ジョセフソン接合でも電流が流れるのです．

このジョセフソン接合を使ってこれから詳しく量子ビットを見ていくのですが，一つ決めなければいけないことがあります．それは何を基準に分解して考えるかということです．なお，この分解した基準のことを基底と言います．基底の取り方は様々なのですが，後こでは電荷の量を下にジョセフソン接合のエネルギーを見ていきます．

基底の取り方

クーパー対が通り抜けて，右に何個行ったか，左に何個行ったかで \(|0\rangle\)と\(|1\rangle\)を区別することは理想的にはできるでしょう．つまり，それぞれ初期状態で右側にいるクーパー対の数を\(N_R\),左側にいるクーパー対の数を\(N_L\)として，トンネル効果によって左の超伝導体から右の超伝導体へ通り抜けたクーパー対の数を\(m\)個とするとし，状態を記述することができます：

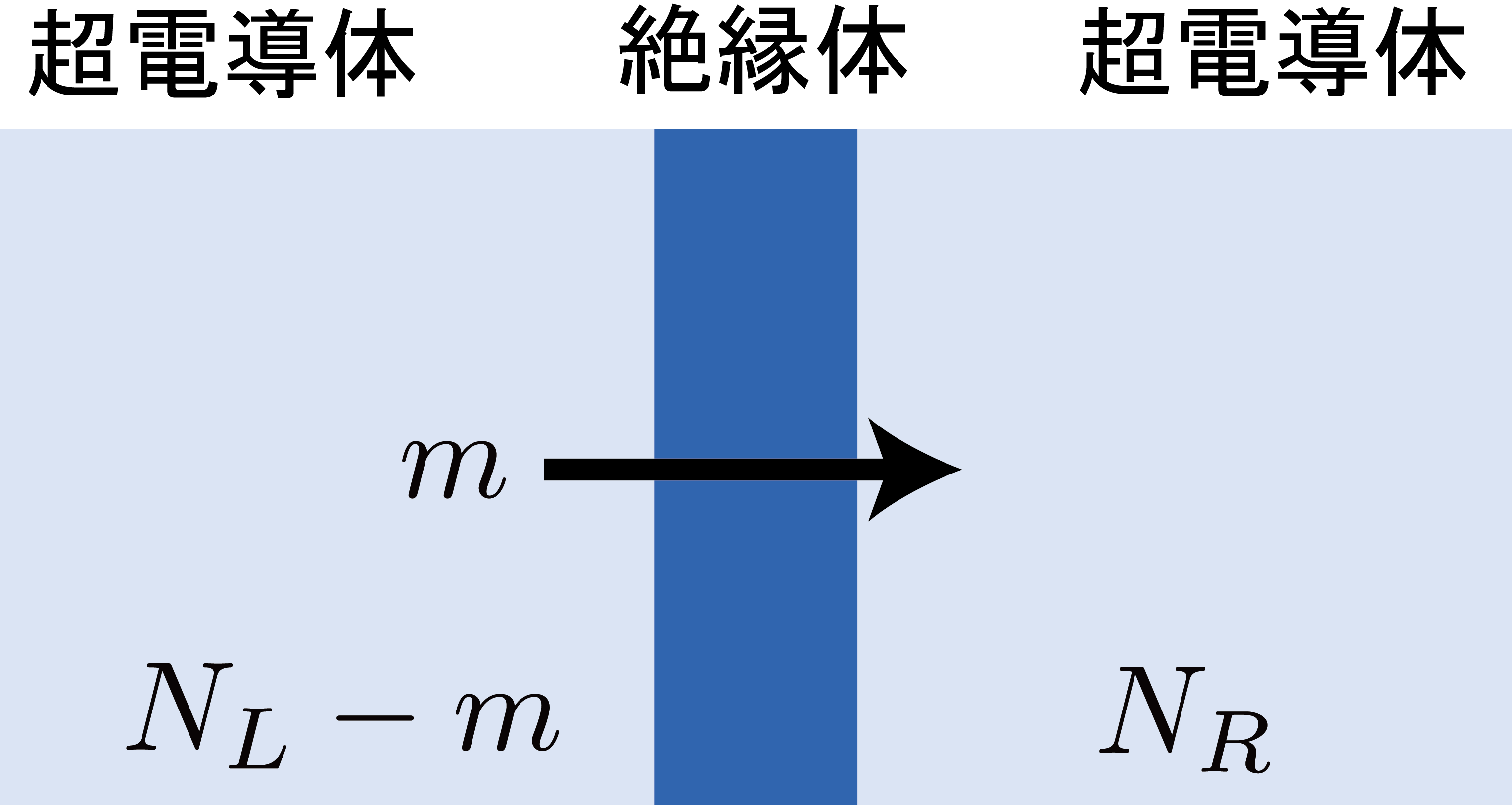
基底の概念図

(26)\[\begin{align} |m\rangle = |N_L-m,N_R+m\rangle. \end{align}\]

この基底より，ジョセフソン接合を通ったクーパー対の数が定義できます．：

(27)\[\begin{align} \hat{n} = \sum_m |m\rangle m\langle m| \end{align}\]

ジョセフソン接合を単位時間当たりのクーパー対の数が電流に比例するため，ジョセフソン接合に流れる電流は

(28)\[\begin{align} \hat{I} = 2e \frac{d\hat{n}}{dt} \end{align}\]

として求めることができます． そして，この基底を利用して，ジョセフソン接合のエネルギーを導出することもでき，以下で与えられます．

ジョセフソン接合のエネルギー

(29)\[\begin{align} -E_J \cos(\phi) \end{align}\]

以下は基底になる説明と，ジョセフソン接合のエネルギーの導出です．
「クーパー対が\(m\)個通り抜ける」状態と「クーパー対が\(m\)個以外通り抜ける」状態は原理的には識別可能なのでそれぞれの状態は直交しています：

(30)\[\begin{align} \langle m | n\rangle=0 \quad \text{for}\quad m\neq n. \end{align}\]

また，

(31)\[\begin{align} \langle m |m \rangle =1 \end{align}\]

と正規化すれば正規直交基底を作ることができます．後で，この正規直交基底を使用して，超伝導量子ビットを見ていきます．
ここで，ジョセフソン接合エネルギーと呼ばれるエネルギー\(E_J\)を，例えば0個が移動した状態の時，右に1個\((|1\rangle)\)と左に1個\((|-1\rangle)\)だけトンネルするためのエネルギーと考えるとジョセフソン接合のハミルトニアンは

(32)\[\begin{align} H = -\frac{1}{2}E_J \sum_{m} \{ |m\rangle \langle m+1| + |m+1\rangle \langle m| \} \end{align}\]

と表すことができます．これはまさに固体物理の強結合近似のモデルと似ており，固有状態はやや天下りですが，位相の部分が現れ

(33)\[\begin{align} |\phi\rangle = \sum_{-\infty}^{\infty} e^{im\phi}|m\rangle \end{align}\]

と表すことができます．実際に\(H|\phi\rangle = E|\phi\rangle\)に代入すると固有値\(E\)は綺麗に以下のように求まります：

(34)\[\begin{align} H|\phi\rangle &= -\frac{1}{2}E_J \sum_{m} \{ |m\rangle \langle m+1| + |m+1\rangle \langle m| \} \sum_{-\infty}^{\infty} e^{im\phi}|m\rangle\\ &= -\frac{1}{2}E_J \sum_{m} \{ |m\rangle \langle m+1|e^{i(m+1)\phi}|m+1\rangle + |m\rangle \langle m-1|e^{i(m-1)\phi}|m-1\rangle \}\\ &= -\frac{1}{2}E_J \sum_{m} \{ e^{i(m+1)\phi} + e^{i(m-1)\phi} \}|m\rangle\\ &= -E_J \cos(\phi) |\phi\rangle. \end{align}\]

よって，ジョセフソン接合のエネルギーが求まりました．