1量子ビットの場合#

第一章では\(X,Y,Z,H,CNOT\)ゲートに関して説明をしました．実は，これらはシュレディンガー方程式：

(1)#\[\begin{align} i\hbar \frac{\partial}{\partial t}|\psi(t)\rangle = H |\psi(t)\rangle \end{align}\]

を解いて得られた量子状態の時間発展の特殊な例にすぎないのです．この章ではどのようなハミルトニアンになるか，どのようにしてシュレディンガー方程式を解くかなどに注目をして，1量子ビットのゲート操作に関して解説をしていきます．

注意

このセクションでは前のセクションで説明した周波数固定型トランズモン量子ビットと呼ばれる量子ビットを扱います．

1量子ビット(概略)#

何ができるようになりたいか？#

第一章で説明をしたようにすべての1量子ビットに対する量子ゲートはすべてBloch球上の回転に対応しています．つまり，\(X,Y,Z\)方向の任意の角度の回転を表す実装ができればすべての1量子ビットに対する量子ゲートを実装することができるでしょう．
ただ，\(X,Y,Z\)3つの軸をすべて実装する必要はなく，実は\(X,Z\)軸の任意の角度の回転だけでBloch球のすべての状態を表現することができるのです．以下の\(U_3\)ゲートは，\(\theta,\phi,\lambda\)の3つの自由度からなるゲートです．この\(U_3\)ゲートによってBloch球の任意の位置を表現できます．

(2)#\[\begin{align} U_3(\theta,\phi,\lambda) = Z_{\phi-\frac{\pi}{2}}X_{\frac{\pi}{2}}Z_{\pi-\theta}X_{\frac{\pi}{2}}Z_{\lambda-\frac{\pi}{2}} \end{align}\]

以上の式を見て分かるように，Bloch球の任意の位置を記述するためには，

\(X_{\frac{\pi}{2}}\)
\(Z_{任意}\) の二つのゲートを実装すればすべてのゲート操作を行うことができるのです．驚くことに\(Y\)ゲートの実装や\(\pi/2\)以外の\(X\)ゲートの回転ゲートの実装は不要になっています．つまり最終的な目標は

最終目標

任意の\(Z\)の回転ゲートと，\(X_{\frac{\pi}{2}}\) を実装すること

です．

実装#

以下の構造のように，量子ビットが\(V(t)\)に繋がっている場合を考えましょう：

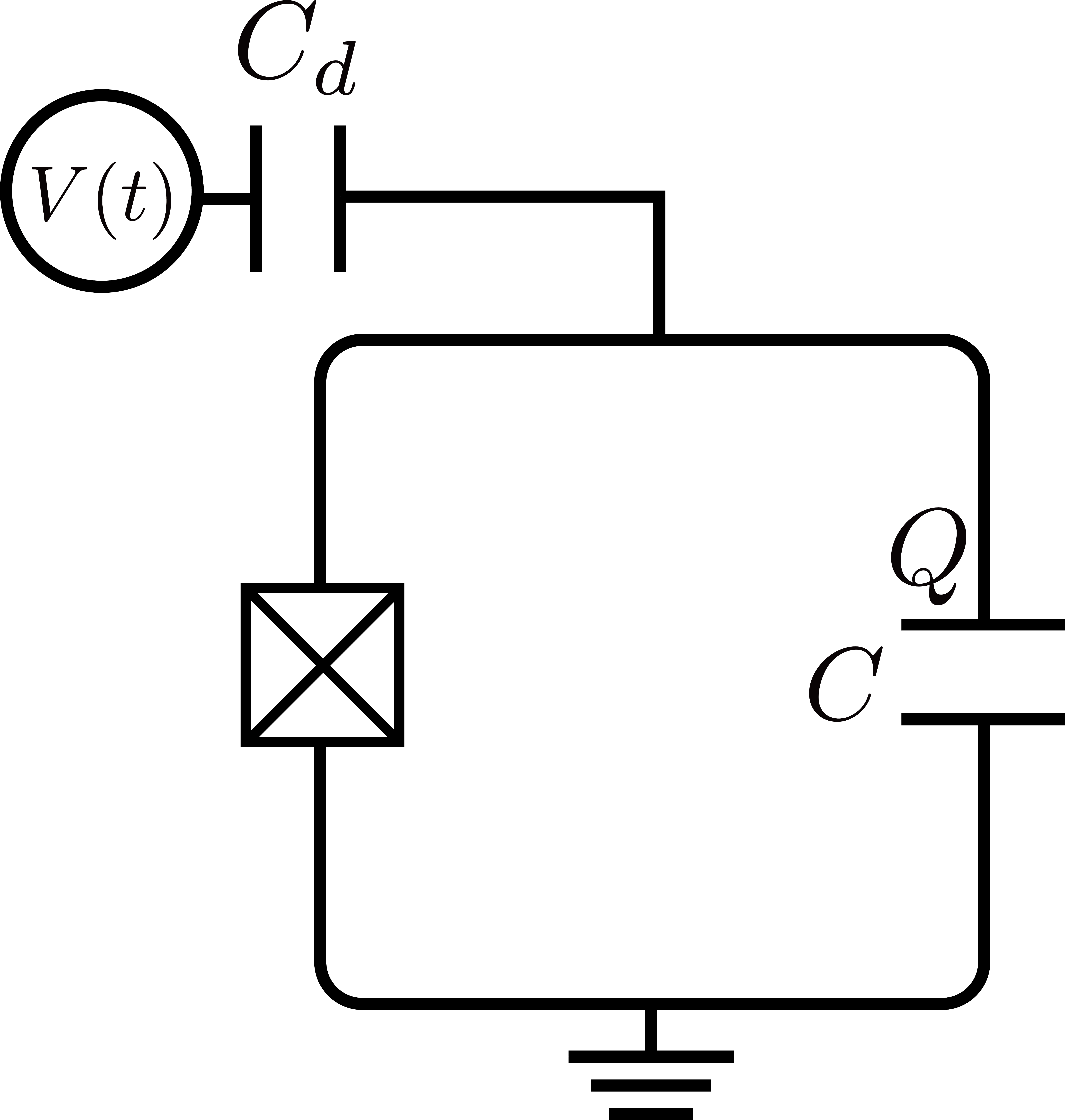
../../../_images/transmon.png — トランズモン量子ビットが\(V(t)\)に繋がっている回路図#

この全体のハミルトニアンは，\(\Omega\)を定数，\(Q\)を量子ビット内の電荷だとして，

(3)#\[\begin{align} H = H_{\text{transmon}} + \hbar V(t)Q\frac{C_d}{C_d + C} \end{align}\]

と表すことができます[Krantz et al., 2019]．このハミルトニアンを下にV(t)によってどのようにして量子状態が変化するかに着目をします．よって，まず第一の目標としては任意の\(V(t)\)に応じて量子ビットの初期状態に対してどのように時間発展をするかを計算をすることです．そこで，前のセクションで取り扱ったように，

(4)#\[\begin{align} Q \to \hat{Q} &= 2e\hat{n} = 2e \left[ \frac{E_J}{32 E_C} \right]^{1/4} \cdot i (\hat{a}-\hat{a}^{\dagger})\\ &=: -iQ'(\hat{a}-\hat{a}^\dagger),\quad Q' = -2e \left[ \frac{E_J}{32 E_C} \right]^{1/4} \end{align}\]

と量子化して代入すると，

(5)#\[\begin{align} H = H_{\text{transmon}} - i\hbar V(t)Q'(a-a^\dagger)\frac{C_d}{C_d + C} \end{align}\]

となります．ここで，前のセクションと同様にして2準位のみに固定すると，\(\hat{a} \to |0\rangle\langle 1|,\hat{a}^\dagger \to|1\rangle\langle 0| \)へ変換することができ，新たに\(\frac{C_d}{C_d + C} Q'= \Omega\)とすると，

(6)#\[\begin{align} H = \underbrace{-\frac{\hbar\omega_q}{2}\sigma_z}_{H_0} + \underbrace{\hbar\Omega V(t)\sigma_y }_{H_d} \label{hamiltonian} \end{align}\]

となります．上式の導出の過程は以下の通りです．

\(H_0\)の項は前のセクションの導出を参考にしてください．以下は\(H_d\)の導出です．

(7)#\[\begin{align} |1\rangle\langle 0| &= \begin{bmatrix} 0 \\ 1 \end{bmatrix} [1,0] = \begin{bmatrix} 0 & 0\\ 1 & 0 \end{bmatrix}\\ |0\rangle\langle 1| &= \begin{bmatrix} 1 \\ 0 \end{bmatrix} [0,1] = \begin{bmatrix} 0 & 1\\ 0 & 0 \end{bmatrix} \end{align}\]

となるので，それぞれを\(-i (a-a^{\dagger})\)に代入すると，

(8)#\[\begin{align} -i (a-a^{\dagger}) = \begin{bmatrix} 0 & -i\\ i & 0 \end{bmatrix} = \sigma_y \end{align}\]

になります．よって導出ができました．

ここからの流れは単純です．このハミルトニアンを使って，シュレディンガー方程式を作ります：

(9)#\[\begin{align} i\hbar \frac{\partial}{\partial t} |\psi(t)\rangle = H |\psi(t)\rangle \end{align}\]

回転系に移る．#

回転系に移るとは，観測する人(カメラ)がある軸を中心に回転をしながら観察するということです．例えば地球に住んでいる我々は地球の自転の軸を中心に回転をしながらすべてを観察しているため回転系に入っていると言えます．
回転系に入ることの恩恵は以下の例を考えると分かりやすいです．例では\(Z\)軸を中心に量子状態がぐるぐる回ってしまっている場合を思い浮かべましょう．くどいようですが，回転系ではない実験室系では量子状態がBloch球上で\(Z\)軸ををぐるぐる回っており，どのようにして状態が変化しているか分かりにくいですが，軸と一緒に回転する回転系に入って観察すると，以下の赤い軌跡のように綺麗に状態が変化していることが分かります．

これからはこのような回転系に入ることで解析をしやすくして理解を深めます．

以下ではこの回転系に入って議論するために，回転演算子というものを定義しておきます：

回転演算子

一般に角振動数\(\omega\)で回転座標系に入るために作用させる演算子は

(10)#\[\begin{align} \hat{U}(t) = \exp\left[ - i \frac{\omega t}{2} \sigma_i\right] \end{align}\]

で与えられます．(\(\sigma_i\)の\(i\)にはそれぞれ\(x,y,z\)などの軸が入ります．)

今回の場合は\(\omega_q\)の角振動数で，\(Z\)軸中心に回転する座標系に移ってみましょう．よって，今回の場合の回転演算子は

(11)#\[\begin{align} \hat{U}_{\text{rf}}(t) := \exp\left[ -i\frac{\omega_q}{2}t\sigma_z \right] = \cos\left( \frac{\omega_q}{2}t \right)\sigma_I - i \sin\left( \frac{\omega_q}{2}t \right)\sigma_z \label{test} \end{align}\]

で与えられます．ある状態\(|\psi(t)\rangle\)があった時にこれが回転系に移ると，

(12)#\[\begin{align} |\psi_{\text{rf}}(t)\rangle := \hat{U}_{\text{rf}}(t)|\psi(t)\rangle \end{align}\]

と変換されるとします．ではこの状態が従うようなシュレディンガー方程式はどのような方程式になり，シュレディンガー方程式から導出されるハミルトニアン(\(\tilde{H}\))はどのような形になるでしょうか．
\(|\psi_{\text{rf}}(t)\rangle\)が従うシュレディンガー方程式は以下のようになります：

(13)#\[\begin{align} i\hbar \frac{\partial}{\partial t} |\psi_{\text{rf}}(t)\rangle &=i\hbar \frac{\partial}{\partial t}\left(\hat{U}_{\text{rf}}(t)|\psi(t)\rangle \right) \\ &= i\hbar \left\{ (\partial_t \hat{U}_{\text{rf}}(t)) |\psi(t)\rangle + \hat{U}_{\text{rf}}(t) ( \partial_t |\psi(t)\rangle ) \right\}\\ &= i\hbar \left\{ \dot{\hat{U}}_{\text{rf}}(t) \hat{U}_{\text{rf}}^{\dagger} (t) |\psi_{\text{rf}}(t)\rangle + \hat{U}_{\text{rf}}(t) \frac{1}{i\hbar} H |\psi(t)\rangle \right\}\\ &= \underbrace{\left\{i\hbar \dot{\hat{U}}_{\text{rf}}(t) \hat{U}_{\text{rf}}^{\dagger} (t) + \hat{U}_{\text{rf}}(t)H \hat{U}_{\text{rf}}^{\dagger} (t) \right\}}_{\tilde{H}} |\psi_{\text{rf}}(t)\rangle\\ &=:\tilde{H}|\psi_{\text{rf}}(t)\rangle \end{align}\]

つまり，以上の式で定義した\(\tilde{H}\)が回転系でのハミルトニアンになります．このハミルトニアンを今考えている系\(\eqref{hamiltonian}\)で求めてみましょう！．
回転演算子の時間発展，共役は式\(\eqref{test}\)より次で与えれれます：

(14)#\[\begin{align} \dot{\hat{U}}_{\text{rf}}(t) &= -i\frac{\omega_q}{2}\sigma_z\exp\left( -i\frac{\omega_q}{2}t\sigma_z \right)= -\frac{\omega_q}{2}\sin\left( \frac{\omega_q}{2}t \right)\sigma_I - i \frac{\omega_q}{2} \cos\left( \frac{\omega_q}{2}t \right)\sigma_z\\ \hat{U}_{\text{rf}}^{\dagger} (t) &= \exp\left( i\frac{\omega_q}{2}t\sigma_z \right)= \cos\left( \frac{\omega_q}{2}t \right)\sigma_I +i \sin\left( \frac{\omega_q}{2}t \right)\sigma_z \end{align}\]

これらを\(\tilde{H}\)に代入すると，

(15)#\[\begin{align} \tilde{H} = \hbar\Omega V(t) \left( \sigma_y \cos(\omega_q t) -\sigma_x \sin(\omega_q t) \right) \end{align}\]

となります．導出は以下の通りです．

(16)#\[\begin{align} \tilde{H} &= i\hbar \dot{\hat{U}}_{\text{rf}}(t) \hat{U}_{\text{rf}}^{\dagger} (t) + \hat{U}_{\text{rf}}(t)H \hat{U}_{\text{rf}}^{\dagger} (t) \\ &= i\hbar \left( -i\frac{\omega_q}{2}\sigma_z\exp\left( -i\frac{\omega_q}{2}t\sigma_z \right) \right) \exp\left( i\frac{\omega_q}{2}t\sigma_z \right) \\ &\quad + \exp\left( -i\frac{\omega_q}{2}t\sigma_z \right) \left( -\frac{\hbar\omega_q}{2}\sigma_z + \hbar\Omega V(t)\sigma_y \right)\exp\left( i\frac{\omega_q}{2}t\sigma_z \right)\\ &= \frac{\hbar\omega_q}{2}\sigma_z -\frac{\hbar\omega_q}{2}\sigma_z + \exp\left( -i\frac{\omega_q}{2}t\sigma_z \right) \hbar\Omega V(t)\sigma_y\exp\left( i\frac{\omega_q}{2}t\sigma_z \right)\\ &=\exp\left( -i\frac{\omega_q}{2}t\sigma_z \right) \hbar\Omega V(t)\sigma_y\exp\left( i\frac{\omega_q}{2}t\sigma_z \right)\\ &=\hbar\Omega V(t) \left(\cos\left( \frac{\omega_q}{2}t \right)\sigma_I - i \sin\left( \frac{\omega_q}{2}t \right)\sigma_z\right) \sigma_y\left(\cos\left( \frac{\omega_q}{2}t \right)\sigma_I + i \sin\left( \frac{\omega_q}{2}t \right)\sigma_z\right)\\ &=\hbar\Omega V(t) \left\{ \sigma_y \left(\cos^2\left( \frac{\omega_q}{2}t \right) -\sin^2\left( \frac{\omega_q}{2}t \right) \right) -\sigma_x \left( 2\sin\left( \frac{\omega_q}{2}t \right)\cos\left( \frac{\omega_q}{2}t \right)\right) \right\}\\ &= \hbar\Omega V(t) \left( \sigma_y \cos(\omega_q t) -\sigma_x \sin(\omega_q t) \right) \end{align}\]

ここで，実際に打つパルスを

(17)#\[\begin{align} V(t) = V_0 \exp\left[ -\frac{(t-t_0)^2}{2\sigma^2} \right]\sin(\omega_d t+ \phi) \end{align}\]

という分布のパルスにしましょう！実際に図示をすると以下のような図になり，\(\sigma\)の値や\(V_0\)や\(\omega_d\)の値を動かすことで，実際のパルスの形を決めることができます．例えば\(\sigma\)は以下の図のようにパルスの幅を決定します．

この\(V(t)\)を\(\tilde{H}\)に代入してみましょう：

(18)#\[\begin{align} \tilde{H} = \hbar V_0 \Omega \exp\left[ -\frac{(t-t_0)^2}{2\sigma^2} \right] \sin(\omega_d t+ \phi)\left( \sigma_y \cos(\omega_q t) -\sigma_x \sin(\omega_q t) \right) \end{align}\]

ここで，三角関数を含む部分のみに注目をして整理すると，以下の式が導出できます．以下では回転波近似という近似を利用しています．

(19)#\[\begin{align} \sin(\omega_d t+ \phi)\left( \sigma_y \cos(\omega_q t) -\sigma_x \sin(\omega_q t) \right) \approx -\frac{1}{2} \sin(\omega_q t - \omega_d t + \phi) \sigma_y -\frac{1}{2}\cos(\omega_q t - \omega_d t + \phi) \sigma_x \end{align}\]

導出と近似方法(回転波近似)は以下の通りです．

(20)#\[\begin{align} &\sin(\omega_d t+ \phi)\left( \sigma_y \cos(\omega_q t) -\sigma_x \sin(\omega_q t) \right) \\ &= \left( \sin(\omega_d t)\cos(\phi) + \cos(\omega_d t)\sin(\phi) \right) \left( \sigma_y \cos(\omega_q t) -\sigma_x \sin(\omega_q t) \right) \\ &= \frac{1}{2}\left[ \left( \sin(\omega_d t + \omega_q t) + \sin(\omega_d t - \omega_q t) \right)\cos(\phi) + \left( \cos(\omega_d t + \omega_q t) + \cos(\omega_d t - \omega_q t)\right) \sin(\phi) \right]\sigma_y\\ &\quad-\frac{1}{2}\left[ \left( -\cos(\omega_d t + \omega_q t) + \cos(\omega_d t - \omega_q t) \right)\cos(\phi) + \left( \sin(\omega_d t + \omega_q t) - \sin(\omega_d t - \omega_q t)\right) \sin(\phi) \right]\sigma_x\\ &\approx \frac{1}{2}\left[ \sin(\omega_d t - \omega_q t)\cos(\phi) +\cos(\omega_d t - \omega_q t) \sin(\phi) \right] \sigma_y \\ &\quad-\frac{1}{2} \left[ \cos(\omega_d t - \omega_q t)\cos(\phi) - \sin(\omega_d t - \omega_q t)\sin(\phi) \right]\sigma_x\\ &= \frac{1}{2}\left[ -\sin(\omega_q t - \omega_d t)\cos(\phi) +\cos(\omega_q t - \omega_d t) \sin(\phi) \right] \sigma_y \\ &\quad-\frac{1}{2} \left[ \cos(\omega_q t - \omega_d t)\cos(\phi) + \sin(\omega_q t - \omega_d t)\sin(\phi) \right]\sigma_x\\ &= -\frac{1}{2} \sin(\omega_q t - \omega_d t + \phi) \sigma_y -\frac{1}{2}\cos(\omega_q t - \omega_d t + \phi) \sigma_x \end{align}\]

上の式では，\(\omega_q\)が\(\omega_d\)のに十分に近く，\(\omega_d + \omega_q\)が\(\omega_d - \omega_q\)に比べて十分に大きく，例えば\(\sin((\omega_d + \omega_q)t) + \sin((\omega_d - \omega_q)t)\)の場合，後で十分に長い時間で積分を行うため，\(\omega_d + \omega_q\)の項が十分に早く振動して平均化して\(0\)になることを利用しています．(これを回転波近似と言います．) よって，他の項も同様にして上式のようになります．

ここで，実際に入射するパルスの周波数\(\omega_d\)をトランズモン量子ビットの周波数\(\omega_q\)に一致させてみましょう．すると，\(\tilde{H}\)は簡単な式になります：

(21)#\[\begin{align} \tilde{H} = -\frac{1}{2}\hbar V_0 \Omega \exp\left[ -\frac{(t-t_0)^2}{2\sigma^2} \right] \left\{ \cos(\phi)\sigma_x + \sin(\phi)\sigma_y \right\} \end{align}\]

このハミルトニアンの場合の時間発展を求めてみましょう！

改めてシュレディンガー方程式は

(22)#\[\begin{align} i\hbar \frac{\partial}{\partial t} |\psi_{\text{rf}}(t)\rangle = \tilde{H}(t)|\psi_{\text{rf}}(t)\rangle \end{align}\]

でした．ここで，\(t=0\)の時の状態は\(|\psi_{\text{rf}}(0)\rangle\)なので，

(23)#\[\begin{align} |\psi_{\text{rf}}(t)\rangle = \exp\left( \frac{1}{i\hbar}\int_0^t \tilde{H}(t')dt' \right)|\psi_{\text{rf}}(0)\rangle \end{align}\]

となります．これに先ほど求めた\(\tilde{H}\)を代入してガウス積分より積分をすると次のようになります：ただし，\(t\)は\(\sigma,t_0\)よりも十分に大きく，\(t_0\)は\(\sigma\)より十分に大きいものとします．

(24)#\[\begin{align} |\psi_{\text{rf}}(t)\rangle &= \exp\left( \frac{i}{2}V_0 \Omega \left\{ \cos(\phi)\sigma_x + \sin(\phi)\sigma_y \right\} \int_0^t\exp\left[ -\frac{(t'-t_0)^2}{2\sigma^2} \right]dt' \right)|\psi_{\text{rf}}(0)\rangle\\ &\approx \exp\left( \frac{i}{2}V_0 \Omega \left\{ \cos(\phi)\sigma_x + \sin(\phi)\sigma_y \right\} \sigma \sqrt{2\pi} \right)|\psi_{\text{rf}}(0)\rangle\\ &= \exp\left( \frac{i}{2}V_0 \Omega \sigma \sqrt{2\pi} \left\{ \cos(\phi)\sigma_x + \sin(\phi)\sigma_y \right\} \right)|\psi_{\text{rf}}(0)\rangle \end{align}\]

なおガウス積分は次の通りです．：

(25)#\[\begin{align} \int_{-\infty}^{\infty} e^{-\alpha x^2}dx = \sqrt{\frac{\pi}{\alpha}} \end{align}\]

\(\theta = - V_0 \Omega\sigma \sqrt{2\pi}, \boldsymbol{n} = (\cos(\phi),\sin(\phi)), \boldsymbol{\sigma} = (\sigma_x, \sigma_y)\)とすると，

(26)#\[\begin{align} |\psi_{\text{rf}}(t)\rangle = \exp\left( -\frac{i}{2} \theta \boldsymbol{n}\cdot \boldsymbol{\sigma} \right)|\psi_{\text{rf}}(0)\rangle \end{align}\]

となることが分かります．これは以下の図のように，ブロッホ球上での\(XY\)平面状で\(\phi\)だけ傾けた向きに\(\theta\)だけ回転することに等しく，回転が実際に入射するパルスの大きさ\(V_0\)などに比例することが分かります．

また，\(t_0,\sigma\)よりも十分に長い\(t\)では上式のように\(|\psi_{\text{rf}}(t)\rangle\)は\(t\)に依存しなくなります．これはパルスを送りブロッホ球上で回転しきることに等しいことで説明がつきます．
実際の実験室では\(V_0\)や\(\sigma\)や\(\phi\)を調整することによって，目的の演算を行うことができるのでます．まとめると回転系での量子状態の時間発展は以下で表されています．

回転系での時間発展

初期状態\(|\psi_{\text{rf}}(0)\rangle\)に対しての時間発展は

(27)#\[\begin{align} |\psi_{\text{rf}}(t)\rangle &= \exp\left( -\frac{i}{2} \theta \boldsymbol{n}\cdot \boldsymbol{\sigma} \right)|\psi_{\text{rf}}(0)\rangle \\ & ただし，\theta = - V_0 \Omega\sigma \sqrt{2\pi}, \boldsymbol{n} = (\cos(\phi),\sin(\phi)), \boldsymbol{\sigma} = (\sigma_x, \sigma_y) \end{align}\]

で与えられます．

元の系に戻る#

上の場合は一つのパルスを送りましたが，他に続けてパルスを送り続けた場合は

(28)#\[\begin{align} |\psi_{\text{rf}}(t)\rangle = 　\cdots\cdot \exp\underbrace{\left( -\frac{i}{2} \theta_2 \boldsymbol{n}_2\cdot \boldsymbol{\sigma} \right)}_{\text{パルス2}}\cdot \exp\underbrace{\left( -\frac{i}{2} \theta_1 \boldsymbol{n}_2\cdot \boldsymbol{\sigma} \right)}_{\text{パルス1}} |\psi_{\text{rf}}(0)\rangle \end{align}\]

となります．先ほど説明したようにそれぞれの\(\theta,\boldsymbol{n}\)を調整することによってブロッホ球を回転させることができます．しかし最後に一つ忘れていることがあります．それはまだ回転系に入っておりもとの系に戻る必要があるということです．例えばパルスを一つ打ち込み\(X\)軸中心に\(-\pi\)だけ回転させた時，\(t=0\)での状態を\(|0\rangle\)とすると，

(29)#\[\begin{align} |\psi_{\text{rf}}(t)\rangle = \exp\left( -\frac{i}{2}(-\pi) \sigma_x \right)|0\rangle \end{align}\]

となりますが，実際の系(実験室系)では，以下のアニメーションのように回転しながら\(X\)軸方向の回転をしています．一方これまで議論してきた回転系では\(Z\)軸を中心に回転する効果がなくBloch球上の状態が変化していることが分かります．

実験室系では\(Z\)方向の回転によって最終的に結果がごちゃごちゃになってしまうのではないかと不安に思う方もいるでしょう．しかし，この回転は問題ないのです．(だからこそ最初に宣言したように私は回転系に入って議論を続けました．)
第一章で説明したように，量子状態の「測定」は\(Z\)軸上の射影測定のみを考えます．つまり，実験室系で\(X,Y\)平面上で回転をしようがしまいが，Z軸への射影測定の結果は変化しないため，回転系上で議論をしても問題ないということです．

以上のことは数式上では次のように説明できます．回転系ではパルスを打つと，回転系では，

(30)#\[\begin{align} |\psi_{\text{rf}}(t)\rangle = (Hゲートのパルス)\cdot (Xゲートのパルス)|0\rangle \end{align}\]

と表されます．元の実験室系に戻ると，\(|\psi_{\text{rf}}(t)\rangle = \hat{U}^{\dagger}_{\text{rf}}|\psi(t)\rangle\)であっため，

(31)#\[\begin{align} |\psi(t)\rangle = \hat{U}^{\dagger}_{\text{rf}}\cdot (Hゲートのパルス)\cdot (Xゲートのパルス)|0\rangle \end{align}\]

となり，最後に回転演算子を作用させたものが実験室系での状態です．すなわち，以下のアニメーションのように，回転系で演算を行い，最後に回転をさせて実験室系に戻ると，ただ単に同じ\(\theta\)上で回転をするだけになり，これは測定結果を変化させることがないということです．

以上の話をより一般的に書くと，

(32)#\[\begin{align} |\psi(t)\rangle = \hat{U}^{\dagger}_{\text{rf}}　\cdots\cdot \exp\underbrace{\left( -\frac{i}{2} \theta_2 \boldsymbol{n}_2\cdot \boldsymbol{\sigma} \right)}_{\text{パルス2}}\cdot \exp\underbrace{\left( -\frac{i}{2} \theta_1 \boldsymbol{n}_2\cdot \boldsymbol{\sigma} \right)}_{\text{パルス1}} |\psi_{\text{rf}}(0)\rangle \end{align}\]

となりますが，実際に測定に関与する状態は\(\hat{U}^{\dagger}_{\text{rf}}\)は関係なく，

(33)#\[\begin{align} |\psi_{\text{rf}}(t)\rangle = 　\cdots\cdot \exp\underbrace{\left( -\frac{i}{2} \theta_2 \boldsymbol{n}_2\cdot \boldsymbol{\sigma} \right)}_{\text{パルス2}}\cdot \exp\underbrace{\left( -\frac{i}{2} \theta_1 \boldsymbol{n}_2\cdot \boldsymbol{\sigma} \right)}_{\text{パルス1}} |\psi_{\text{rf}}(0)\rangle \end{align}\]

であるのです．

回転系に入るという動作を行うことによって綺麗にそれぞれのゲート操作を簡潔に説明することができました．よって，以下にまとめることができます．

回転系に入ることの意味

全体にかかってしまう\(Z\)軸中心の回転の影響を除去できて解析が簡単になる．

私が勘違いしてたこと：回転系の効果が見える？

第一章では，\(Z\)測定の他に\(X\)測定などの概念を紹介しました．すると．たしかに回転系に入った場合と実験室系では\(Z\)測定の結果は変化しないが，ある時間だけ遅らせて\(H\)測定をして，量子状態がぐるぐる回る様子も観察できないか？とこれを初めて勉強した時，思っていました．
結論から言うと，その様子を観察することはできません．というのも，Hゲートは回転系で定義されたゲートであり，実験室系で定義されていないからです．すなわち，\(H\)ゲートを作用させてH測定をしたいと思っても，実験室系では\(H\)ゲートさえもぐるぐる回転してしまうため，実験室系で定義された\(H\)ゲートは実現されないのです．

\(X_{\frac{\pi}{2}}\)ゲート#

最終目標の一つである\(X_{\frac{\pi}{2}}\)ゲートの実現方法を説明していきます，\(X_{\frac{\pi}{2}}\)とは\(X\)軸を中心に\(\pi/2\)だけ回転させるゲート操作です．
ということです．回転系の量子の状態は式(\(\eqref{Rotation_hamiltonian}\))より，

(34)#\[\begin{align} |\psi_{\text{rf}}(t)\rangle= \exp\left( -\frac{i}{2}\theta \left\{ \cos(\phi)\sigma_x + \sin(\phi)\sigma_y \right\} \right)|\psi_{\text{rf}}(0)\rangle \end{align}\]

でした．つまり，\(\phi=0\)となるようなパルスを打ち込み，\(\theta\)の結果がちょうど\(\pi/2\)だけ回転させているようなパルスの振幅を見つければ良いということになります．このようなパルスを調整して正確なゲートを行える値を探し，それぞれの量子ビットに対してその正確な値を保存しておくことで，\(X_{\frac{\pi}{2}}\)ゲートを実現できます．この流れをキャリブレーションと言います．

キャリブレーション#

それでは量子ビットに入射するパルスの振幅\(V_0\)の値を変えて実験することでキャリブレーションを行いましょう！
本来であれば実際の量子コンピュータを使用しますが，後で説明する複数量子ビットで分かりやすい説明をするため，Qiskit Dynamicsというモジュールを用いて数値計算を行います．

バックエンドを定義する#

まずはどのようなバックエンドを使用するかを定義します．

# バックエンドのモデル
ibm_backend = Fake7QPulseV1()

# 使用するソルバー

qubits_to_model = [0,1,2,3,4]
solver_options = {
    "method": "jax_odeint",
    "atol": 1e-6,
    "rtol": 1e-8,
    "hmax": ibm_backend.configuration().dt}
    
# 数値計算を行うバックエンド
backend = DynamicsBackend.from_backend(
    backend=ibm_backend,
    subsystem_list=qubits_to_model,
    solver_options=solver_options,
    )

バックエンドからデフォルトの周波数を取り出す．#

パルスを送信するためには各量子ビットの周波数である\(\omega_q\)の値が必要でした．1番目に割り当てられている量子ビット(量子ビット0)の周波数を取り出すと以下の通りになります．

backend_defaults = ibm_backend.defaults()

# 単位の定義
GHz = 1.0e9
MHz = 1.0e6
us = 1.0e-6
ns = 1.0e-9

# 以下の量子ビットについて量子ビット周波数を探索する
qubit1 = 0

# 量子ビット0に関しての周波数を取り出す．
center_frequency1_Hz = backend_defaults.qubit_freq_est[qubit1] 
print(f"量子ビット{qubit1}は {center_frequency1_Hz / GHz}GHz の周波数です．")

量子ビット0は 5.260483791030155GHz の周波数です．

パルスの形を決定する．#

パルスには\(V_0,\sigma,t_0,\omega_d,\phi\)の値，そしてパルスを出力している時間\(t_f\)が必要でした：

(35)#\[\begin{align} V(t) = V_0 \exp\left[ -\frac{(t-t_0)^2}{2\sigma^2} \right]\sin(\omega_d t+ \phi) \end{align}\]

(図を挿入) また，\(t_0\)の値は理想的に\(t_0=t_f/2\)になっているとすると，最終的にはパルスには\(V_0,\sigma,t_f,\omega_d,\phi\)の値が必要になります．それぞれ定義していきましょう．
今回は\(X\)軸を中心に回転させてキャリブレーションを行うため，\(V_0\)は\(0から0.3\)まで変化させる値とします：

V_0_min = 0
V_0_max = 0.3
num_x90_points = 200

V_0 = np.linspace(V_0_min, V_0_max, num_x90_points)

\(\sigma\)は0.015usであるとし，\(t_f\)は\(\sigma\)の\(8\)倍にすることで，ガウシアンが端で切れてしまう効果を弱くします．また\(\phi\)も設定します：

sigma = 0.015 * us
t_f = sigma * 8
phi = 0

パルスを設定する．#

(x90_calibration)という名前のパルスを量子ビット0に登録します．(drive_duration)と，(drive_sigma)にさきほど設定した\(t_f,\sigma\)を設定し，このパルスの周波数に当たる\(\omega_d\)を量子ビット0の周波数である(center_frequency1_Hz)を設定します．

# V_0をパラメータとする．
drive_amp = Parameter('drive_amp')

# パルスを設定する．
with pulse.build(backend=backend, default_alignment='sequential', name='x90_calibration') as x90_calibration_sched:
    # 量子ビット0を登録する．
    drive_chan = pulse.drive_channel(qubit1)
    # t_f
    drive_duration = pulse.seconds_to_samples(t_f)
    # sigma
    drive_sigma = pulse.seconds_to_samples(sigma)
    # 周波数
    pulse.set_frequency(center_frequency1_Hz, drive_chan)
    # 位相
    pulse.set_phase(phi,drive_chan)

    # パルスを打つ
    pulse.play(pulse.Gaussian(duration=drive_duration,
                              amp=drive_amp,
                              sigma=drive_sigma,
                              name='x90_calibration'), drive_chan)

量子回路を作成する．#

今回のキャリブレーションでは，(1)初期状態を\(|0\rangle\)として(2)先ほど定義した(x90_calibration)のパルスを当てて(3)測定します．

# パルスに対応するカスタムゲートを作成する．
x90_calibration = Gate("x90_calibration", 1, [drive_amp])

# 量子回路を作成 今回は1つの量子ビットが必要
qc_x90_calibration = QuantumCircuit(1)

# 初期状態は|0>であるため(2)を行う
qc_x90_calibration.append(x90_calibration, [0])
# (3)を行う
qc_x90_calibration.measure_all()

######################################
# カスタムゲートにパルスを対応させる．
qc_x90_calibration.add_calibration(x90_calibration, (0,), x90_calibration_sched, [drive_amp])
# 振幅V0を設定した範囲でキャリブレーションを行う
exp_x90_calibration_circs = [qc_x90_calibration.assign_parameters({drive_amp: a}, inplace=False) for a in V_0]
# バックエンドの設定で必要な操作
backend.target.add_instruction(
    x90_calibration,
    {(0,): InstructionProperties(calibration=x90_calibration_sched)},
)

量子回路は以下の通りになります．

qc_x90_calibration.draw('mpl')

../../../_images/6b6ef4bca855efc6b77d47e29e4b57e883142e4cf3dd7ee6d776d1806c74c855.png

パルスは以下のようになり，量子ビット0に(x90_calibration)というパルスを当てて，桃色の測定用のパルスを当てていることが分かります．

exp_x90_schedule = schedule(exp_x90_calibration_circs[-1], ibm_backend)
exp_x90_schedule.draw()

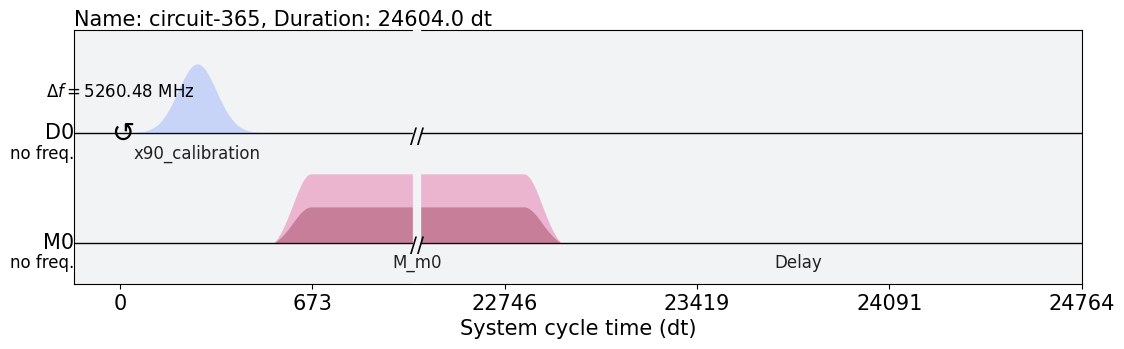
../../../_images/b2421698ca454f99055007440105a6f0e37770805828aff9dd96d67de6fdb3b2.png

シミュレーションを行う．#

各振幅で500回測定を行いその平均値を返すとします．(以下のコードのnum_shots_per_pointが各振幅での測定回数でmeas_return='avg’で平均値を返すようにしています．)

import warnings
warnings.filterwarnings('ignore')
num_shots_per_point = 500
job = backend.run(exp_x90_calibration_circs,
            meas_level=2,
            meas_return='avg',
            shots=num_shots_per_point)
job_monitor(job)

Show code cell output Hide code cell output

---------------------------------------------------------------------------
KeyboardInterrupt                         Traceback (most recent call last)
Cell In[11], line 4
warnings.filterwarnings('ignore')
num_shots_per_point = 500
----> 4 job = backend.run(exp_x90_calibration_circs,
           meas_level=2,
           meas_return='avg',
           shots=num_shots_per_point)
job_monitor(job)

File ~\Desktop\qualsimu-textbook-new\.venv2\lib\site-packages\qiskit_dynamics\backend\dynamics_backend.py:452, in DynamicsBackend.run(self, run_input, validate, **options)
job_id = str(uuid.uuid4())
dynamics_job = DynamicsJob(
   backend=backend,
   job_id=job_id,
   (...)
   },
)
--> 452 dynamics_job.submit()
return dynamics_job

File ~\Desktop\qualsimu-textbook-new\.venv2\lib\site-packages\qiskit_dynamics\backend\dynamics_job.py:54, in DynamicsJob.submit(self)
if self._result is not None:
   raise JobError("Dynamics job has already been submitted.")
---> 54 self._result = self._fn(job_id=self.job_id(), **self._fn_kwargs)
self._time_per_step["COMPLETED"] = datetime.now()

File ~\Desktop\qualsimu-textbook-new\.venv2\lib\site-packages\qiskit_dynamics\backend\dynamics_backend.py:472, in DynamicsBackend._run(self, job_id, t_span, schedules, measurement_subsystems_list, memory_slot_indices_list, num_memory_slots_list)
if y0 == "ground_state":
   y0 = Statevector(self._dressed_states[:, 0])
--> 472 solver_results = self.options.solver.solve(
   t_span=t_span, y0=y0, signals=schedules, **self.options.solver_options
)
# compute results for each experiment
experiment_names = [schedule.name for schedule in schedules]

File ~\Desktop\qualsimu-textbook-new\.venv2\lib\site-packages\qiskit_dynamics\solvers\solver_classes.py:532, in Solver.solve(self, t_span, y0, signals, convert_results, **kwargs)
   if self.model.array_library not in ["numpy", "jax", "jax_sparse"]:
       warn(
           "Attempting to internally JAX-compile simulation of schedules, with "
           'Solver.model.array_library not in ["numpy", "jax", "jax_sparse"]. If an error '
           "is not raised, explicitly set array_library at Solver instantation to one of "
           "these options to remove this warning."
       )
--> 532     all_results = self._solve_schedule_list_jax(
       t_span_list=t_span_list,
       y0_list=y0_list,
       schedule_list=signals_list,
       convert_results=convert_results,
       **kwargs,
   )
else:
   all_results = self._solve_list(
       t_span_list=t_span_list,
       y0_list=y0_list,
   (...)
       **kwargs,
   )

File ~\Desktop\qualsimu-textbook-new\.venv2\lib\site-packages\qiskit_dynamics\solvers\solver_classes.py:662, in Solver._solve_schedule_list_jax(self, t_span_list, y0_list, schedule_list, convert_results, **kwargs)
for idx, sig in enumerate(all_signals):
   all_samples[idx, 0 : len(sig.samples)] = np.array(sig.samples)
--> 662 results_t, results_y = jit_sim_function(
   unp.asarray(t_span),
   unp.asarray(y0),
   unp.asarray(all_samples),
   unp.asarray(y0_input),
   y0_cls,
)
results = OdeResult(t=results_t, y=results_y)
if y0_cls is not None and convert_results:

KeyboardInterrupt: 

結果を表示してキャリブレーションを完了する．#

シミュレーションが終わったので結果を表示します．まずはそれぞれ\(0,1\)を得た確率を表示します．

たしかに振幅\(V_0\)によってそれぞれの確率が振動する様子を観察できました！\(0\)の確率を三角関数でフィッティングさせて，\(X_{\pi/2}\)を行えるパルスの振幅を求めましょう．
実際にフィッティングすると\(X_{\pi/2}\)を行えている振幅は

0.030798154536926158

となっておりフィッティング結果を図示すると分かるようにフィッティングできていることが分かります．

\(X_{\pi/2}\)のまとめ#

よって以上のようにキャリブレーションを行い\(X_{\frac{\pi}{2}}\)ゲートを実現できるような振幅を各量子ビットで求めて辞書のように保存しているのです．実際に\(X_{\pi/2}\)ゲートを作用させて測定を行った時を考えます．(Qiskit上では\(S_X\)ゲートと呼ばれており，\(X\)に平方根を取ったよなゲートになります．)

qc = QuantumCircuit(1)
qc.sx(0)
qc.measure_all()
qc.draw('mpl',style="clifford")

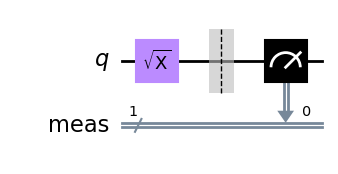
../../../_images/f58d7e57308f18d05be1fd9723550a5282cf49e486ddba08dcf635cf7a8aedc3.png

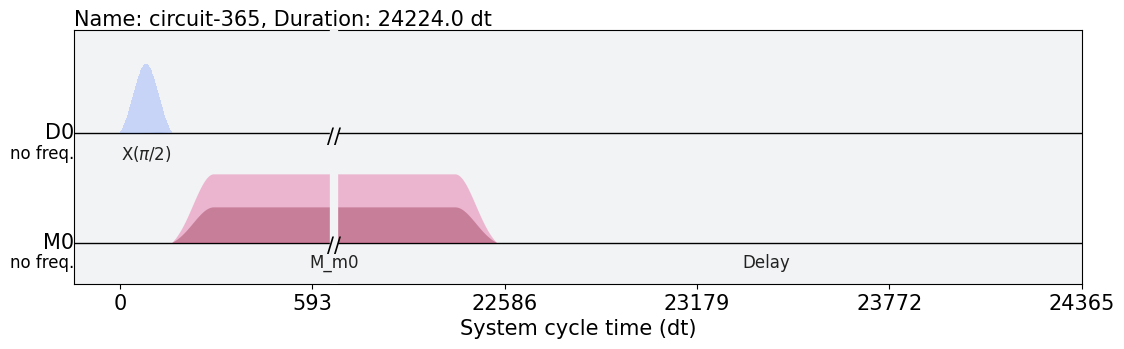
これをパルスレベルまで分解すると以下の表が得られます．一段目は\(X_{\pi/2}\)ゲートのパルスで，二段目は測定用のために打っているパルスです．たしかに，\(X_{\pi/2}\)ゲート自体はただ一つのパルスだけで実装されていることが分かります．このパルスの振幅は今キャリブレーションで求めたパルスの振幅になっているのです．

qc_trans = transpile(qc, ibm_backend)
pulse_schedule = schedule(qc_trans, ibm_backend)
pulse_schedule.draw()

../../../_images/9cfdadb36f85fc3928065950d0e0ea59137057105088e4d708182088971be57b.png

\(Z_{\theta}\) ゲート#

\(X_{\frac{\pi}{2}}\)ゲートは比較的簡単に実現ことができました．しかし問題は\(Z\)ゲートです．

(36)#\[\begin{align} |\psi_{\text{rf}}(t)\rangle= \exp\left( -\frac{i}{2}\theta \left\{ \cos(\phi)\sigma_x + \sin(\phi)\sigma_y \right\} \right)|\psi_{\text{rf}}(0)\rangle \end{align}\]

の中には\(Z\)軸方向を中心に回転できるような演算は見当たりません．(もし\(\exp\)の中に\(\sigma_z\)が含まれているとすると，\(Z\)軸中心に回転を行うことができるのですが…) そこで提案されており2023年現在実際に使われているのが仮想Zゲートという方法です．
\(X_{\frac{\pi}{2}}\)ゲートの説明をする時に，\(\phi\)は\(\phi=0\)で固定すると話しました．つまり，1つ目のパルスも，2つ目のパルスもそれぞれ打つパルスは\(\phi=0\)で固定をします．例えば以下のようになります：

(37)#\[\begin{align} (1つ目のパルス): V(t) &= V_0 \exp\left[ -\frac{(t-t_0)^2}{2\sigma^2} \right]\sin(\omega_d t+ {\color{red}0} )\\ (2つ目のパルス): V'(t) &= V'_0 \exp\left[ -\frac{(t-t_0)^2}{2\sigma'^2} \right]\sin(\omega_d t+ {\color{red}0} ) \end{align}\]

しかし実際にパルスを生成する際には最初に\(\phi=0\)で決定したらもう変更ができないわけではなく，\(\phi\)の部分を各パルスで変更させることが可能です．つまり，どの向きを\(X\)軸にするかという基準を変えることができます．\(X\)軸の基準が変わるということがまさしく\(Z\)ゲートを操作させることと等価になっているのです．
つまり，\(\phi＝\phi'\)で\(\theta\)だけ回転させたゲートを\(X_{\theta}^{(\phi')}\)などと書くことにすると，(以下は行列計算で確かめることができます．)

(38)#\[\begin{align} X_{\theta_2}^{(\phi')}X_{\theta_1} = Z_{\phi'}X_{\theta_2}Z_{-\phi'}X_{\theta_1} \end{align}\]

となっています．(\(Z_{\phi'}\)は最後に\(z\)軸を中心に回転させているだけなので測定結果に影響を与えません．) この例から見て分かるように，\(\phi'\)だけ基準をずらすと，\(-\phi'\)だけ\(z\)軸上に回転することが分かります．

実際の例を見てみましょう．初期状態\(|0\rangle\)に対して\(\phi=0\)で\(X_{\pi/2}\)を作用させ，次に \(\phi=\pi/3\) で \(X_{\pi/4}\) (つまり，\( X_{\pi/4}^{(\pi/3)})\) をさせた時，これは\(X_{\pi/2}\)を作用させて，\(Z_{-\pi/3}\)を作用させ，最後に\(X_{\pi/4}\)を作用させたものに等しくなっています．以下のアニメーションでは，左側が理想的なゲート操作，左側が仮想Zゲートの流れになっています．それぞれ矢印を動かして測定結果が同じになることを確認してみてください：

注意点としては，基準を変更したので基準を変えた場所から今後すべてのゲートの位相を変化させなくてはいけません．つまり，\(X_{\theta_2}^{(\phi')}X_{\theta_1}\)に対して\(Y\)ゲートを作用させたいと思ったら，\(Y^{(0)}\)ゲートではなくて，\(Y^{(\phi')}\)ゲートを作用させる必要があり，以下のようにたしかに，\(X_{\theta_1} \to Z_{-\phi'} \to X_{\theta_2} \to Y\)の順番で作用していることが分かります．

(39)#\[\begin{align} Y^{(\phi')}X_{\theta_2}^{(\phi')}X_{\theta_1} &= Z_{\phi'}YZ_{-\phi'} \left(Z_{\phi'}X_{\theta_2}Z_{-\phi'}X_{\theta_1}\right)\\ &= Z_{\phi'} Y X_{\theta_2}Z_{-\phi'}X_{\theta_1} \end{align}\]

以上から分かるように仮想\(Z\)ゲートは次の性質を持ちます．

仮想\(Z\)ゲートの性質

\(Z\)ゲートはパルス不要であるため，エラー率や実行時間という概念がない．

そのため，1量子ビットを演算する際に実際のそれぞれの量子ビットに必要な情報は\(X_{\frac{\pi}{2}}\)を実現する\(\theta =- V_0 \Omega\sigma \sqrt{2\pi}\)をキャリブレーションした情報のみで良いことになります．

以上で見たように，\(Z_{\theta}\)ゲートは基本的に位相を変化させるだけで追加のパルスを必要としません．実際にパルスを必要としないことを見てみましょう．以下は\(Z\)軸中心に\(\pi\)だけ回転させる演算を\(|0\rangle\)に作用させて測定する回路です．

qc = QuantumCircuit(1)
qc.rz(np.pi,0)
qc.measure_all()
qc.draw('mpl',style="clifford")

../../../_images/82ffed880f4dd5093f2a98f5bdf7ef0c2ecd7ec29b2dd9ac8c7a74e24f3739dd.png

そして，パルスの様子を見てみると，以下のように\(Z_\theta\)ゲートではパルスを加えていないことが分かります．以下でパルスが加えられいるのは測定用のパルスです．

qc_trans = transpile(qc, ibm_backend)
pulse_schedule = schedule(qc_trans, ibm_backend)
pulse_schedule.draw()

../../../_images/c266da55cca7ad2414aca7b2f39a33d60026daa9949fe4b2cb1a40b78d2052a6.png

他のゲート#

他のゲート操作は\(X_{\frac{\pi}{2}}\)と\(Z\)ゲートの2つを使って操作することができます．最初に説明したように以下の\(U_3\)ゲートを使って一般的にどの軸で回転させたいかを指定させて各量子ゲートを作成をすることができます：

(40)#\[\begin{align} U_3(\theta,\phi,\lambda) = Z_{\phi-\frac{\pi}{2}}X_{\frac{\pi}{2}}Z_{\pi-\theta}X_{\frac{\pi}{2}}Z_{\lambda-\frac{\pi}{2}} \end{align}\]

例えば\(Y_{\theta}\)ゲートであれば，

(41)#\[\begin{align} Y_{\theta} &= Z_{-\frac{\pi}{2}}X_{\frac{\pi}{2}}Z_{\pi-\theta}X_{\frac{\pi}{2}}Z_{-\frac{\pi}{2}}\\ H &=Z_{\frac{\pi}{2}}X_{\frac{\pi}{2}}Z_{\frac{\pi}{2}} \end{align}\]

となり，たしかに\(X_{\frac{\pi}{2}},Z_\theta\)のみで実装ができることが分かります．

1量子ビットの場合

目次

1量子ビットの場合#

1量子ビット(概略)#

何ができるようになりたいか？#

実装#

回転系に移る．#

元の系に戻る#

\(X_{\frac{\pi}{2}}\)ゲート#

キャリブレーション#

バックエンドを定義する#

バックエンドからデフォルトの周波数を取り出す．#

パルスの形を決定する．#

パルスを設定する．#

量子回路を作成する．#

シミュレーションを行う．#

結果を表示してキャリブレーションを完了する．#

\(X_{\pi/2}\)のまとめ#

\(Z_{\theta}\) ゲート#

他のゲート#