トランズモン量子ビット#

概略#

\(|0\rangle\)と\(|1\rangle\)はそれぞれ量子の状態です．つまり量子の状態が現れるような物理現象でなければいけません．実は，超伝導と呼ばれる現象が現れるようにある回路を冷やしていくと，回路の量子状態がよく見えるようになります．(これを巨視的な量子状態と言います．)
それがゆえに超伝導量子ビットでは超伝導という性質を利用しています．まずは超伝導量子ビットの全体像を見てみましょう．

超伝導量子ビットの回路構造#

超伝導量子コンピュータの量子ビットは回路を作ることで実現できます．超伝導量子ビットの中で，IBMやGoogleや理研などで使われている量子ビットはトランズモン量子ビットと呼ばれています．トランズモン量子ビットの構造は以下の図のようにキャパシタと呼ばれる素子と前のセクションで説明したジョセフソン接合と呼ばれる素子でできています．

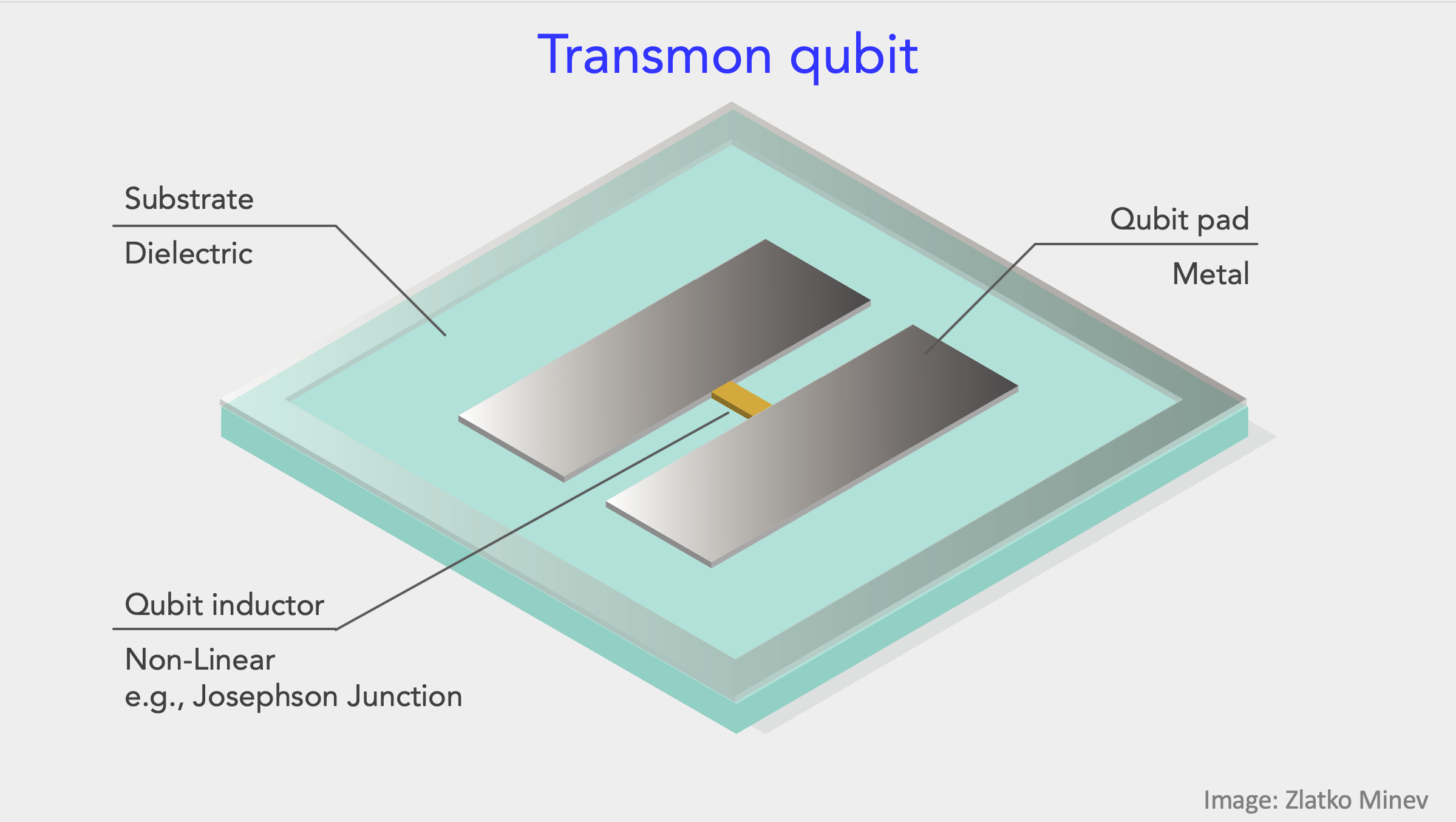
../../../_images/Edz4eluXoAIuvjd.png — トランズモン量子ビットの模式図こちらより引用#

以上の図が1つの量子ビットとなっており，それぞれの量子ビットを接続させることで複数量子ビットの計算を行うことができるのです．以下の図はIBMで使われている量子コンピュータの基盤の図で，この図では7個の量子ビットが集積化さています．

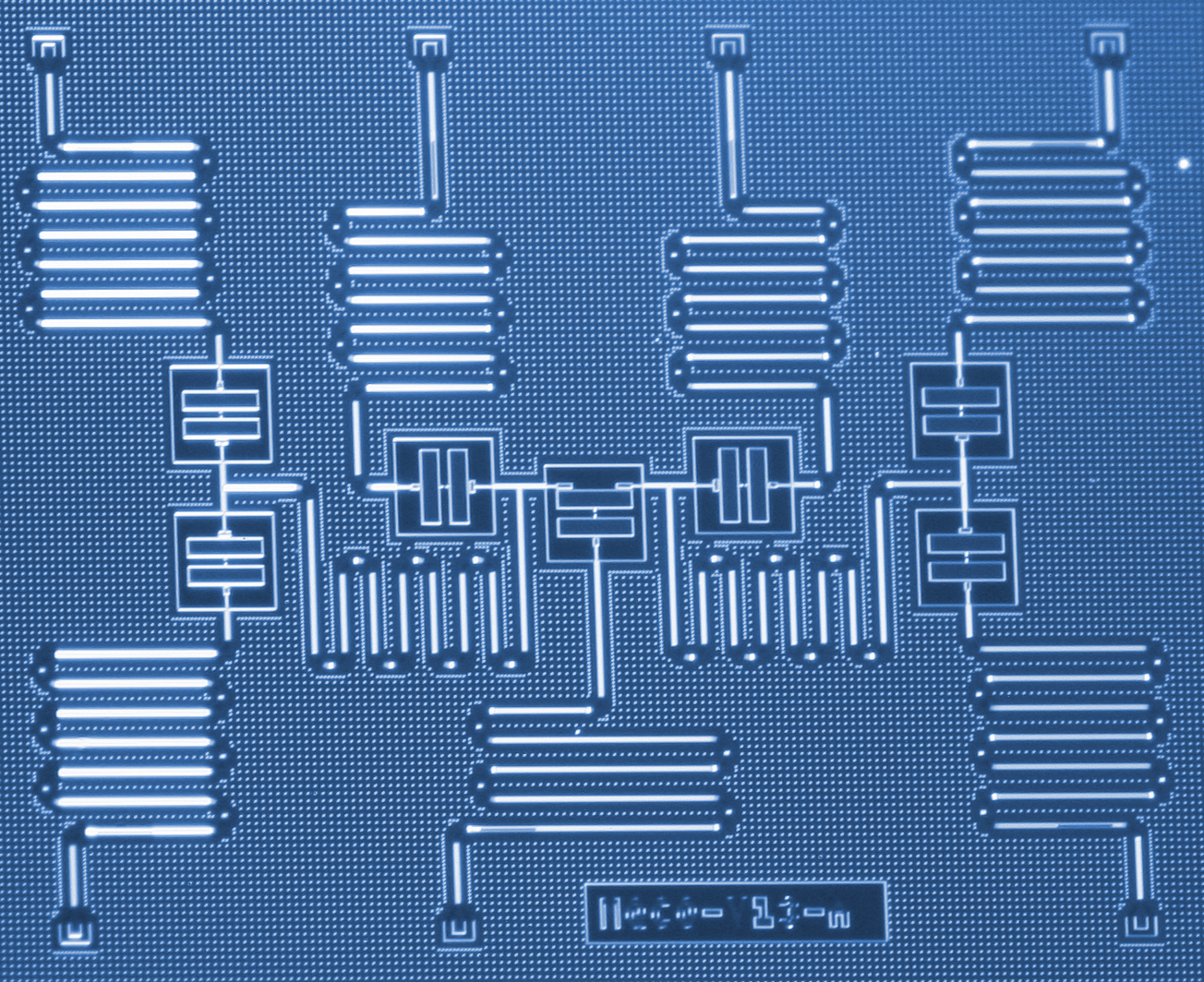
../../../_images/qchem_device_blue.jpg — 集積化されたトランズモン量子ビットの写真.IBMホームページより引用．#

トランズモン量子ビットに関して説明をしていくわけですが，扱いを簡単にするため上図の1量子ビットの図をより単純な回路としてとらえると以下の回路図にすると以下の通りになります．なお，バツ印のような素子はジョセフソン接合を表しています．一見回路と回路図が異なるように見えるかもしれませんが，それぞれ等価です：

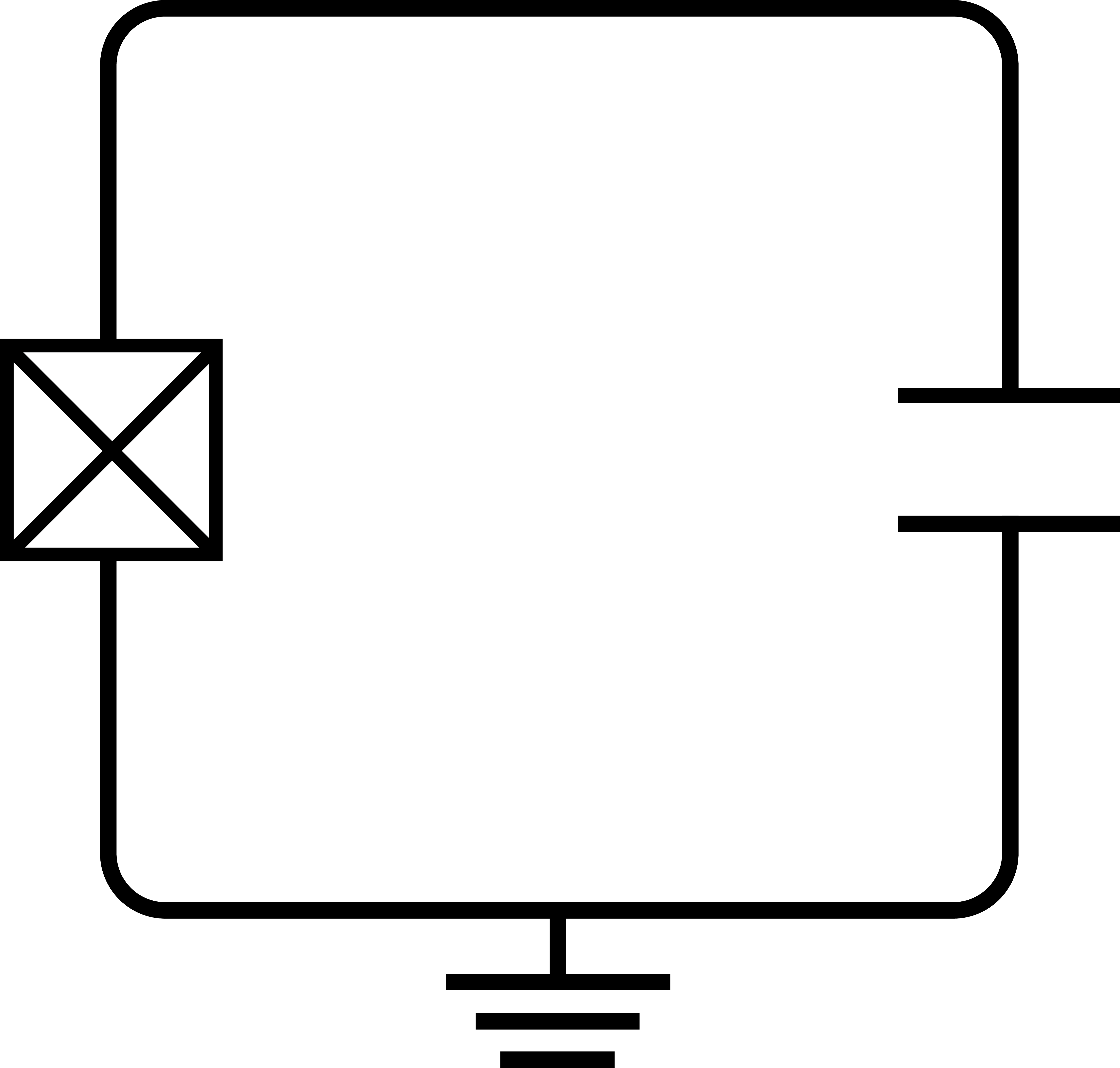
../../../_images/transmon_2.png — トランズモン量子ビットの回路図#

この回路のハミルトニアンはLC共振器のインダクタをジョセフソン接合に変化させたものに等しく，LC共振器の全体のハミルトニアンのインダクタの項を前のセクションで求めたジョセフソン接合の項に置き換えれば，トランズモン量子ビットのハミルトニアンを導出できます：

(1)#\[\begin{align} H = 4E_C\hat{n}^2 -E_J\cos(\hat{\phi})\quad ただし，E_J/E_C \sim 30 \end{align}\]

注意点

\(E_J/E_C \sim 30\)という条件がトランズモン量子ビットでは必要です．仮に\(E_J/E_C\)が十分に\(0\)に近いと電荷量子ビットと呼ばれる別の量子ビットになります．

なぜ，ジョセフソン接合が必要か？#

LC共振器をそのまま量子ビットとして作用させることはできませんでした．実は，ジョセフソン接合を用いることでLC共振器の問題を解決できるのです．ジョセフソン接合を用いることで，以下の図のようにエネルギーの感覚が不均一になります．

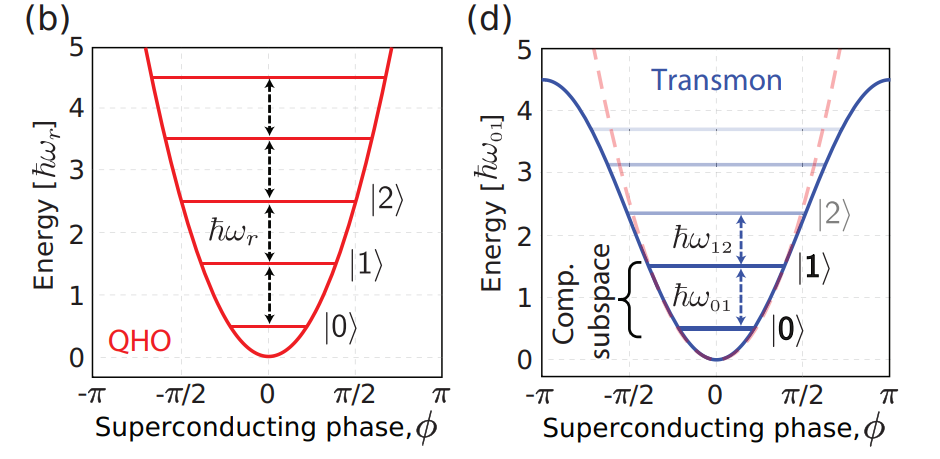
../../../_images/potential.png — LC共振器とトランズモン量子ビットのエネルギー準位の比較図　[Krantz *et al.*, 2019]より引用#

実際にLC共振器と近似したトランズモン量子ビットの固有エネルギーは以下の通りになります．

(2)#\[\begin{align} (LC共振器のエネルギー固有値): E_n &:= \hbar\omega\left( n + \frac{1}{2} \right)\\ (トランズモン量子ビットのエネルギー固有値): E_n &:= \hbar\omega\left(n+ \frac{1}{2}\right) - E_J - \frac{E_C}{2} \left( n^2- n \right) \end{align}\]

以上からエネルギー間隔は以下のようになりたしかに，トランズモン量子ビットの場合はエネルギー間隔が不均一になることが分かります．

(3)#\[\begin{align} (LC共振器のエネルギー間隔): E_{n+1}-E_n &= \hbar\omega \\ (トランズモン量子ビットのエネルギー間隔): E_{n+1}-E_n &= \hbar\omega + \frac{E_C}{2} +\frac{E_C}{2} (-2n+1)\\ &= \hbar\omega - E_C n + \frac{3E_C}{2} \end{align}\]

なお，以下は近似したトランズモン量子ビットの固有エネルギーの導出です．

(もっと知りたい人のために)近似したトランズモン量子ビットのエネルギー固有値の導出方法

マクローリン展開より，

(4)#\[\begin{align} \cos\hat{\phi} \approx 1 - \frac{\hat{\phi}^2}{2} + \frac{1}{24}\hat{\phi}^4 \end{align}\]

となります．よってこれを下のハミルトニアンに代入すると，

(5)#\[\begin{align} H &\approx 4E_C \hat{n}^2 - E_J \left( 1 - \frac{\hat{\phi}^2}{2} - \frac{1}{24}\hat{\phi}^4 \right)\\ &= \underbrace{ 4E_C \hat{n}^2 + \frac{E_J}{2}\hat{\phi}^2 }_{E_J=E_L の場合のLC共振器のハミルトニアン} - E_J + \frac{E_J}{24}\hat{\phi}^4 \end{align}\]

となります．よって，LC共振器のエネルギー固有値は既にもとまっているため，\(- E_J + \frac{1}{24}\hat{\phi}^4\)の項がトランズモン量子ビット固有の項であると言えます．つまり，この項の固有値を求めることができれば全体の固有値を求めることができるでしょう．

ここで，前のセクションで説明したように，\(E_J=E_L\)とした時，

(6)#\[\begin{align} \hat{n} &= \left[ \frac{E_J}{32E_C} \right]^{1/4}\cdot i (\hat{a}-\hat{a}^{\dagger}),\\ \hat{\phi} &= \left[ \frac{2E_C}{E_J} \right]^{1/4}\cdot (\hat{a}+\hat{a}^{\dagger}) \end{align}\]

と置くことができるため，

(7)#\[\begin{align} H &= \hbar\omega\left(\hat{a}^{\dagger}\hat{a}+ \frac{1}{2}\right) - E_J - \frac{E_C}{12}\left( \hat{a}+\hat{a}^{\dagger} \right)^4\\ &\approx \hbar\omega\left(\hat{a}^{\dagger}\hat{a}+ \frac{1}{2}\right) - E_J - \frac{E_C}{2} \hat{a}^{\dagger}\hat{a}^{\dagger}\hat{a}\hat{a} \end{align}\]

となります．(やや専門的な近似ですが，ここでの近似は，対角成分である，\(\hbar\omega\left(\hat{a}^{\dagger}\hat{a}+ \frac{1}{2}\right) \)が，非対角成分である\(\hat{a}\)と\(\hat{a}^\dagger\)の数が一致しない項に比べて非常に大きく，非対角の成分を無視しています．)
よって，

(8)#\[\begin{align} [\hat{a},\hat{a}^\dagger] =1 \end{align}\]

であるため，

(9)#\[\begin{align} H &= \hbar\omega\left(\hat{a}^{\dagger}\hat{a}+ \frac{1}{2}\right) - E_J - \frac{E_C}{2} \hat{a}^{\dagger}( \hat{a}\hat{a}^\dagger-1 )\hat{a}\\ &= \hbar\omega\left(\hat{a}^{\dagger}\hat{a}+ \frac{1}{2}\right) - E_J - \frac{E_C}{2} \left( (\hat{a}^{\dagger}\hat{a})^2- \hat{a}^{\dagger}\hat{a} \right) \end{align}\]

となり，\(\hat{a}^\dagger\hat{a} =\hat{n}\)であるため，

(10)#\[\begin{align} E_n = \hbar\omega\left(n+ \frac{1}{2}\right) - E_J - \frac{E_C}{2} \left( n^2- n \right) \end{align}\]

という固有値の値が得られます．

このようにしてそれぞれのエネルギー間隔が異なるようにすることで，\(E_0,E_1\)間の遷移をしている間に\(E_1,E_2\)間の遷移が起きることはほとんどなくなります．というのも，次のセクションで詳しく説明しますが，量子ビットの状態を遷移させる際にはそれぞれのエネルギー間隔に対応する周波数を持つパルスを当てる必要があり，\(E_0,E_1\)間の遷移をするために当てるパルスを当てる際，パルスの周波数が\(E_1,E_2\)間の周波数と大きく異なるため影響を受けないからです．それが故に\(E_0,E_1\)の状態のみを選択的に取り扱うことが可能なのです．

また，実際には外からノイズとしての電場がかかっておりこれをゲート電圧\(n_g\)として表現すると，ハミルトニアンは以下になります．

(11)#\[\begin{align} H = 4E_C\left(\hat{n}-n_g \right)^2 -E_J\cos(\phi) \end{align}\]

2準位を取り出す．#

(12)#\[\begin{align} H = -\frac{\hbar\omega}{2}\sigma_z \end{align}\]

導出は以下の通りですが，ややアドバンストな内容になるため飛ばしても構いません．

(もっと知りたい人のために)2準位に制限した場合のトランズモン量子ビットの導出方法

さきほど導出したエネルギー固有値ではハミルトニアンを生成消滅演算子\(\hat{a},\hat{a}^{\dagger}\)を使用してトランズモン量子ビットのハミルトニアンを書き換えました：

(13)#\[\begin{align} H \approx \hbar\omega\left( \hat{a}\hat{a}^{\dagger} + \frac{1}{2} \right)-E_J - \frac{E_C}{2}\hat{a}^{\dagger}\hat{a}^{\dagger}\hat{a}\hat{a} \end{align}\]

ここで，2準位に制限しているので，\(- \frac{E_C}{2}\hat{a}^{\dagger}\hat{a}^{\dagger}\hat{a}\hat{a}=0\)になるため，

(14)#\[\begin{align} H \approx \hbar\omega\hat{a}\hat{a}^{\dagger} + \hbar\omega\frac{1}{2}-E_J \end{align}\]

になります．昇降演算子の性質より

(15)#\[\begin{align} \hat{a}|0\rangle &= 0 \quad & \hat{a}|1\rangle = |0\rangle,\\ \hat{a}^{\dagger}|0\rangle &= |1\rangle \quad & \hat{a}^{\dagger}|1\rangle = 0 \end{align}\]

であるため，

(16)#\[\begin{align} \hat{a} &= \begin{bmatrix} 0 & 1\\ 0 & 0 \end{bmatrix}\\ \hat{a}^{\dagger} &= \begin{bmatrix} 0 & 0\\ 1 & 0 \end{bmatrix} \end{align}\]

と表すことができます．(各自計算は代入して確かめてみてください．)以上の行列より，

(17)#\[\begin{align} \hat{a}\hat{a}^{\dagger} + \hat{a}^{\dagger}\hat{a}= \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} =: \sigma_I \end{align}\]

となるため，

(18)#\[\begin{align} \hat{a}^{\dagger}\hat{a} &= \frac{1}{2}\hat{a}^{\dagger}\hat{a} + \frac{1}{2}\hat{a}^{\dagger}\hat{a}\\ &= \frac{1}{2}\hat{a}^{\dagger}\hat{a} + \frac{1}{2}\left( \sigma_I- \hat{a}\hat{a}^{\dagger} \right)\\ &= \frac{1}{2} \left( \hat{a}^{\dagger}\hat{a} - \hat{a}\hat{a}^{\dagger} \right) + \frac{1}{2}\sigma_I\\ & = -\frac{1}{2}\sigma_z + \frac{1}{2}\sigma_I \end{align}\]

となります．ここで，元のハミルトニアンに代入し，単位行列を\(\frac{1}{2}\sigma_I \to \frac{1}{2}\)などとして表記すると，

(19)#\[\begin{align} H = -\frac{\hbar\omega}{2}\sigma_z + \hbar\omega-E_J \end{align}\]

となり，\(\hbar\omega-E_J\)の部分は全体のエネルギーが上下にシフトするだけなので無視することができ，最終的にハミルトニアンは

(20)#\[\begin{align} H =-\frac{\hbar\omega}{2}\sigma_z \end{align}\]

となります．

また，この場合のハミルトニアンの時間発展は例えば時刻\(0\)で状態が\(|0\rangle\)の時

(21)#\[\begin{align} |\psi(t)\rangle = \exp\left( \frac{1}{i\hbar}H \cdot t \right)|0\rangle \end{align}\]

になります．第一章で導出をした次の行列指数関数の性質1を利用すると：

行列指数関数の性質1

(22)#\[\begin{align} \exp( -\frac{i}{2}\theta \sigma_i ) = \cos\left(\frac{\theta}{2}\right)\sigma_I - i \sin\left(\frac{\theta}{2}\right)\sigma_Z \end{align}\]

(23)#\[\begin{align} |\psi(t)\rangle &= \exp( -\frac{i}{2}(-\omega t) \sigma_Z ) |0\rangle\\ &= \left( \cos\left(\frac{-\omega t}{2}\right)\sigma_I - i \sin\left(\frac{-\omega t}{2}\right)\sigma_Z \right)|0\rangle\\ &= \left( \cos\left(\frac{-\omega t}{2}\right)- i \sin\left(\frac{-\omega t}{2}\right) \right)|0\rangle\\ &= \exp\left( i \frac{\omega t}{2} \right)|0\rangle \end{align}\]

となり\(\exp\left( i \frac{\omega t}{2} \right)\)の部分はglobal phaseとなっており測定に関与しないため，たしかに時間発展によって\(|0\rangle\)の状態は保存されていることが分かります．これはただ単にハミルトニアンの固有状態が\(|0\rangle,|1\rangle\)であるということだけなので特別なことは言っておりませんが念のために確認しました．

トランズモン量子ビットをより細かく見てみる．#

ここから先はより詳しくトランズモン量子ビットを見ていき以下を知ることを最終目標とします．

最終目標

トランズモン量子ビットでの量子ビットである\(|0\rangle,|1\rangle\)はそれぞれトランズモン量子ビット内ではどのようになっているか？

前のページにて定義したように，それぞれある状態で右側にいるクーパー対の数を\(N_R\),左側にいるクーパー対の数を\(N_L\)として，トンネル効果によって左の超伝導体から右の超電導体へ通り抜けたクーパー対の数を\(m\)個とするとして基底を作りました：

(24)#\[\begin{align} |m\rangle = |N_L-m,N_R+m\rangle. \end{align}\]

これによって，それぞれ，\(\hat{n}\)と\(E_J\cos(\phi)\)は

(25)#\[\begin{align} \hat{n} &= \sum_m |m\rangle m\langle m|\\ E_J\cos(\phi) &= \frac{1}{2}E_J \sum_{m} \{ |m\rangle \langle m+1| + |m+1\rangle \langle m| \} \end{align}\]

になります．\(\hat{n}\)は\(\hat{n}|m\rangle = m|m\rangle\)になることより確かめられ，\(E_J\cos(\phi)\)は前のセクションで導出しました．よってハミルトニアンは\(I\)を単位行列として，

(26)#\[\begin{align} H = 4E_C\left(\sum_m |m\rangle m\langle m|-n_g I \right)^2 -\frac{1}{2}E_J \sum_{m} \{ |m\rangle \langle m+1| + |m+1\rangle \langle m| \} \end{align}\]

と表現することができます．例えば基底の分解数を\(5\)個に制限して基底を以下のように取り，

(27)#\[\begin{align} |-2\rangle &= [1,0,0,\cdots]^T\\ |-1\rangle &= [0,1,0,\cdots]^T\\ |0\rangle &= [0,0,1,0\cdots]^T\\ \vdots |2\rangle &= [0,\cdots,0,1]^T\\ \end{align}\]

ハミルトニアンを行列で表すことができます．この行列で表現されたハミルトニアンの固有値がエネルギーの固有値の値，そして，固有状態がエネルギーに対する量子の状態となるのです．

数値計算#

よって，このハミルトニアンの行列の固有値と固有状態を\(n_g\)に応じて求めます．ただ，実際の行列の固有値は特殊な場合のみしか解析的に求まりません．そこで今回は解析的に求めず数値計算で求めています．なお，\(E_J/E_C\)の値は\(30\)を用いることにします．
固有エネルギーは\(n_g\)に対してそれぞれ求まります．一番エネルギーが小さいエネルギーである基底エネルギー，二番目に大きいエネルギーである第一励起エネルギー，三番目に大きいエネルギーである第二励起エネルギーは以下の図のように，\(n_g\)によらずほとんど一定の値を取っていることが分かります．

それでは，固有状態はどのようになるでしょうか？これまでクーパー対の偏りの基底で行列を作成しました．ある固有状態(例えば基底エネルギーなど)に対して定義される固有状態は，クーパー対の偏りの重ね合わせ状態になっています．つまり，

(28)#\[\begin{align} (ある固有エネルギーの固有状態) =\cdots \alpha_{-2} |-2\rangle + \alpha_{-1} |-1\rangle + \alpha_0 |-0\rangle + \cdots \end{align}\]

となっており，この固有状態をもう少し分かりやすく説明すると，

(29)#\[\begin{align} &\quad \vdots\\ &|\alpha_{-2}|^2 の確率で，クーパー対は左に2個偏っている．\\ &|\alpha_{-1}|^2 の確率で，クーパー対は左に1個偏っている．\\ &|\alpha_{0}|^2 の確率で，クーパー対は偏りがない．\\ &\quad \vdots \end{align}\]

となります．それぞれの固有エネルギー(基底エネルギー，第一励起エネルギー,第二励起エネルギー) の各基底での確率を取り出すことで各固有状態における物理的な描像が分かるため，それぞれの固有状態をプロットしました．それぞれのボタンを押してその様子を観察してみてください．

つまり，量子ビットの\(|0\rangle\)である\(|g\rangle\)は物理的にどんな状態ですか？と聞かれたら，\(n_g=0\)の場合は，上図より，

(30)#\[\begin{align} &約0.42 の確率でクーパー対の偏りがない\\ &約0.23 の確率でクーパー対は左右に1個ずつ偏っている\\ &約0.043 の確率でクーパー対は左右に2個ずつ偏っている \end{align}\]

状態の重ね合わせ状態と表現することができます．
また，量子ビットの\(|1\rangle\)である\(|e\rangle\)は物理的にどんな状態ですか？と聞かれたら，\(n_g=0\)の場合は，上図より，

(31)#\[\begin{align} &約0.28 の確率でクーパー対は左右に1個ずつ偏っている\\ &約0.18 の確率でクーパー対は左右に2個ずつ偏っている \end{align}\]

状態の重ね合わせ状態と表現することができます．

よって以上のように，トランズモン量子ビットでの\(|g\rangle,|e\rangle\)の物理的な描像を見ることができ，このセクションの目標を達成することができました．

トランズモン量子ビット

目次

トランズモン量子ビット#

概略#

超伝導量子ビットの回路構造#

なぜ，ジョセフソン接合が必要か？#

2準位を取り出す．#

トランズモン量子ビットをより細かく見てみる．#

数値計算#